Q2 - Merge Sorted Arrays

Write a function that accepts an array of sorted arrays, each containing integers. The function should merge these arrays into a single list, ensuring that the integers in this merged list are arranged in ascending order. The provided input array is certain to contain subarrays and each subarray is certain to be non-empty.

Input: arrays = [
  [1, 4, 5],
  [1, 3, 4],
  [2, 6],
]
Output: [1, 1, 2, 3, 4, 4, 5, 6]

Input: arrays = [
  [-1, 1, 5],
  [0, 2],
  [4, 10],
  [-10, 42]
]
Output: [-10, -1, 0, 1, 2, 4, 5, 10, 42]

Input: arrays = [
  [3, 3, 3],
  [3],
  [3],
]
Output: [3, 3, 3, 3, 3]

Solution 1

The key to the first solution's algorithm is efficiently tracking and updating the indices of the current smallest elements in each input array and always choosing the smallest available element to add to the final sorted array. This is not the optimal solution because the optimal solution will use a MinHeap data structure.

Below we will go over the intuition behind our Solution-1 using Example-2. The diagrams below should help the reader have a better understanding of the algorithm.

Iteration 0

• smallestElementIdxs contains four items, each corresponding to an input array. This array tracks the index of the smallest yet-to-be-merged item in each array. Initially, the smallest item in each array is at the first position (index 0). Therefore, at the start, smallestElementIdxs is set to [0, 0, 0, 0], indicating that we are currently considering the first element of each array.

Iteration 1

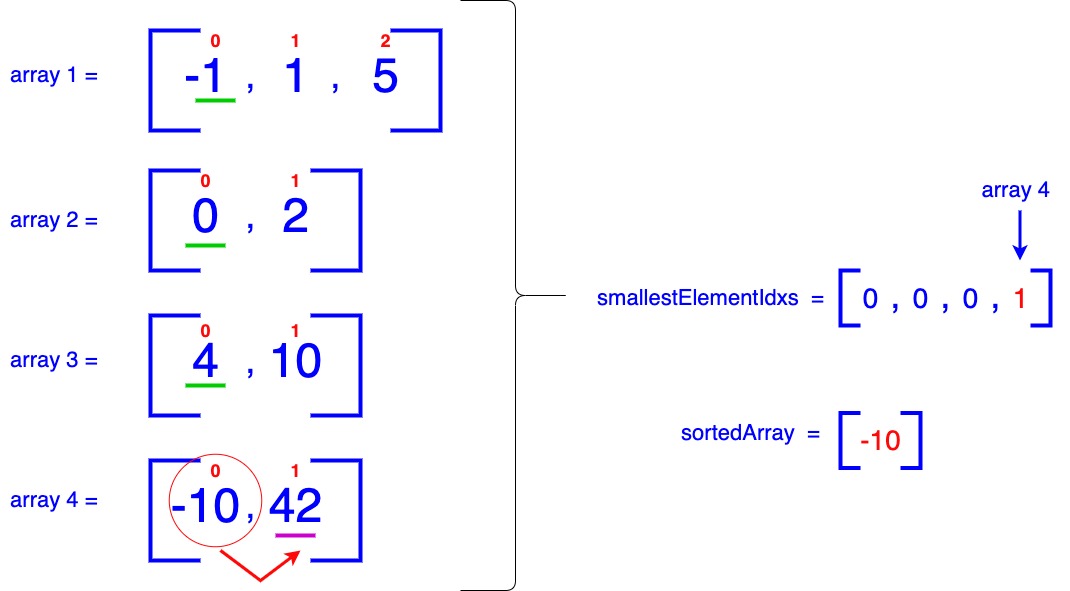
• In the first iteration, we compare the smallest items from every array, which are currently positioned at index 0 in each array. We identify that -10 from array-4 is the smallest among these items. Consequently, we add -10 to our sortedArray. We then increment the corresponding entry in the smallestElementIdxs at index = 3 (which is associated with array-4). This increment indicates that we should now consider the item at index = 1 in array-4 for the next iteration.

Iteration 2

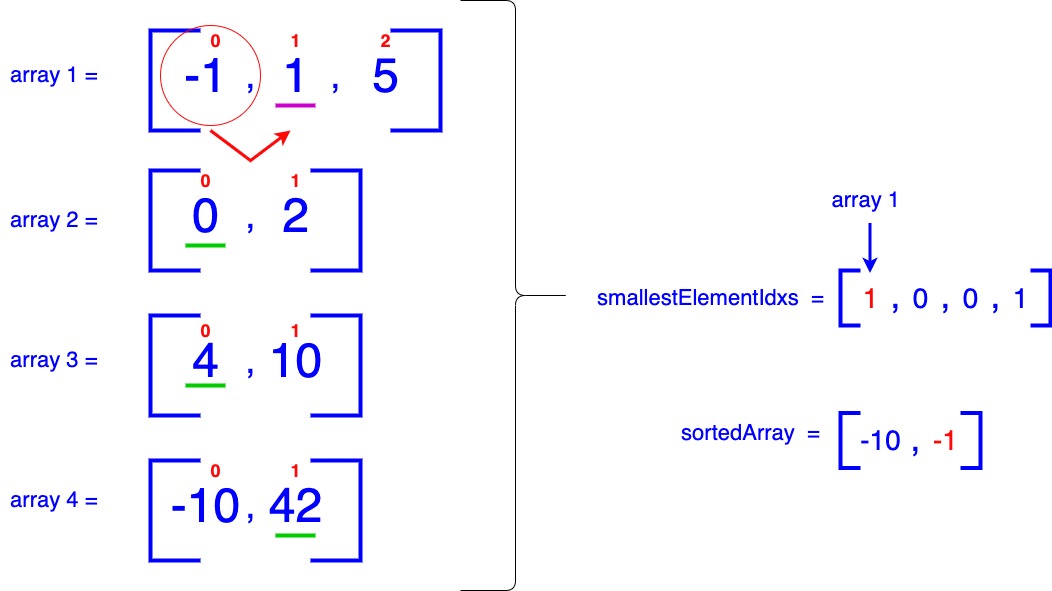
• We identify that -1 from array-1 is the current smallest item. Consequently, we add -1 to our sortedArray. We then increment the corresponding entry in the smallestElementIdxs at index = 0 (which is associated with array-1). This increment indicates that we should now consider the item at index = 1 in array-1 for the next iteration.

Iteration 3

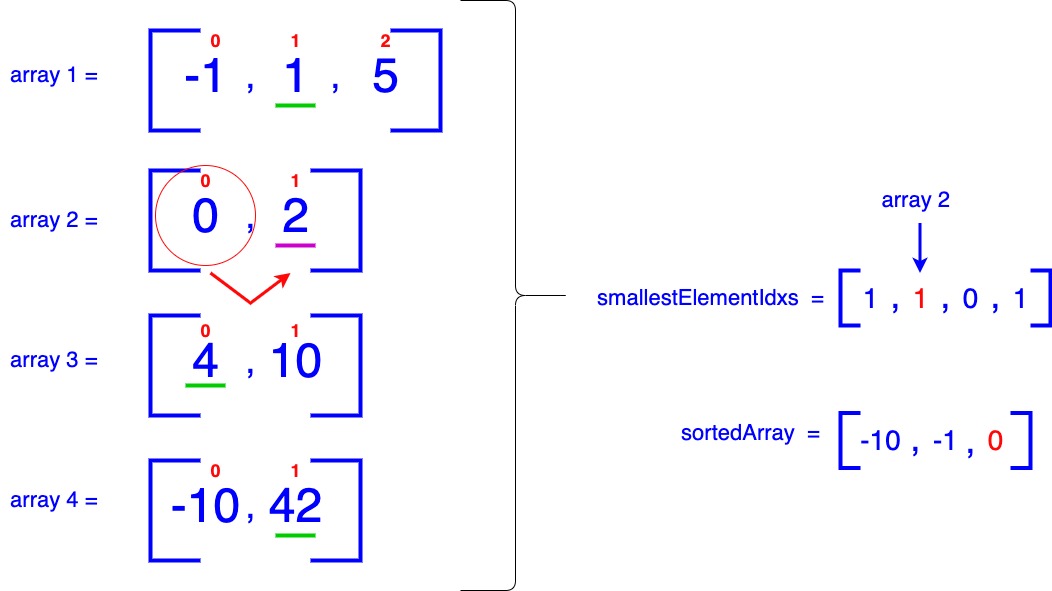
• We identify that 0 from array-2 is the current smallest item. Consequently, we add 0 to our sortedArray. We then increment the corresponding entry in the smallestElementIdxs at index = 1 (which is associated with array-2). This increment indicates that we should now consider the item at index = 1 in array-2 for the next iteration.

Iteration 4

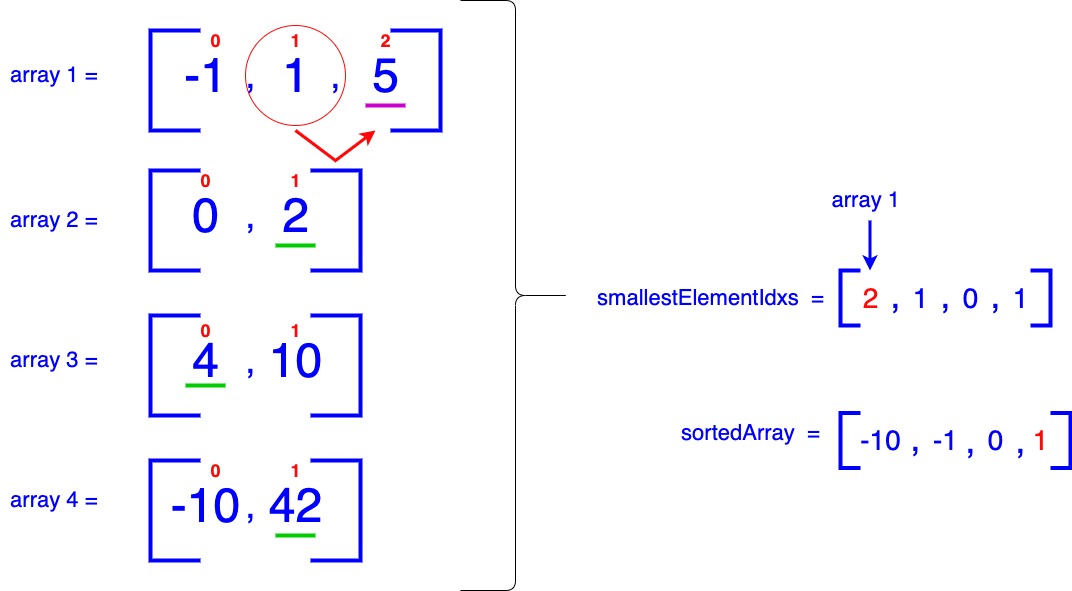
• We identify that 1 from array-1 is the current smallest item. Consequently, we add 1 to our sortedArray. We then increment the corresponding entry in the smallestElementIdxs at index = 0 (which is associated with array-1). This increment indicates that we should now consider the item at index = 2 in array-1 for the next iteration.

We proceed with this process until all the arrays are completely exhausted. This means our final sortedArray will contain all the items from each of the input arrays, merged in sorted order. Below we will go through the time and space complexity of Solution-1.

Complexity Analysis

• Time Complexity: O(nk), where n represents the total number of items across all arrays, and k is the total number of input arrays.

  Explanation:

  1. Iterating Through Items

     • We must iterate through all items to add a total of n items to our final sorted list.

  2. Identifying the Smallest Item

     • For each item, we iterate through k arrays to identify the smallest item in each iteration.

  Combining these steps, the overall time complexity is O(nk), which includes iterating through all items and checking each array in each iteration.

• Space Complexity: O(n + k). The space complexity is mainly influenced by the storage requirements of the sorted array and the indices array.

  Explanation:

  1. Final Sorted Array

     • We need to store a total of n items in our final sorted array.

  2. Indices Array

     • The smallestElementIdxs array, which has a length of k, is used to track the smallest item in each input array at any given point in time.

  Therefore, the overall space complexity is O(n + k), accommodating the necessary data structures for efficient processing.

# O(nk) time | O(n + k) space
def merge_sorted_arrays(arrays):
    sortedArray = [] # Final sorted array.
    # For each array, we store the current smallest item's idx. 
    smallestElementIdxs = [0] * len(arrays)
    while True:
        curr_smallest_elements = []
        for array_idx in range(len(arrays)):
            curr_array = arrays[array_idx]
            # Smallest element's index in current array.
            curr_array_min_idx = smallestElementIdxs[array_idx]
            # We are not done with this array.
            if curr_array_min_idx != len(curr_array):
                # Store a tuple containing current array's min element together with its index.
                curr_smallest_elements.append((array_idx, curr_array[curr_array_min_idx]))
        # We have exhausted all the arrays.
        if len(curr_smallest_elements) == 0: return sortedArray

        # Find the (array_idx, curr_array_item) tuple with the smallest curr_array_item.
        next_smallest_idx_element_tuple = min(curr_smallest_elements, key=lambda x: x[1])
        # Add the newly found smallest item in our final array.
        sortedArray.append(next_smallest_idx_element_tuple[1])
        # We know which array had the current smallest item, so increment its index.
        smallestElementIdxs[next_smallest_idx_element_tuple[0]] += 1

Solution 2 (MinHeap)

Below, we present the optimal solution to our problem. We are using a MinHeap data structure in our algorithm. If you are not familiar with the MinHeap data structure, we strongly suggest that you go through this resource before trying to understand this solution. After going through the provided resource, you will be ready to understand our solution.

import heapq

# O(nlog(k)) time | O(n + k) space
def merge_sorted_arrays(arrays):
    sorted_array = [] # Final sorted array.
    smallest_items = []  # For each array, we store the current smallest item's idx/value.
    
    # Initial smallest items are the very first items in each array.
    for array_idx in range(len(arrays)):
        # Store a tuple containing curr array's min item together with curr array's idx and its smallest item's idx.
        smallest_items.append((arrays[array_idx][0], (array_idx, 0)))
    heapq.heapify(smallest_items) # it's now a minHeap.
    while len(smallest_items) > 0:
        # Current min item, the idx of the array containing it, and the min item's idx itself.
        min_item, idx_info = heapq.heappop(smallest_items)
        array_idx, item_idx = idx_info
        sorted_array.append(min_item)
       
        # We have exhausted this particular array.
        if item_idx == len(arrays[array_idx]) - 1: continue

        # We need to add the next min item of this array together with its idx and also the idx of the array.
        new_item = (arrays[array_idx][item_idx + 1], (array_idx, item_idx + 1))
        heapq.heappush(smallest_items, new_item)
        
    return sorted_array

Below we will go over the intuition behind our Solution-2 using Example-2 from above. The diagrams below should help the reader have a better understanding of this optimal algorithm that relies on MinHeap implementation.

Initialization

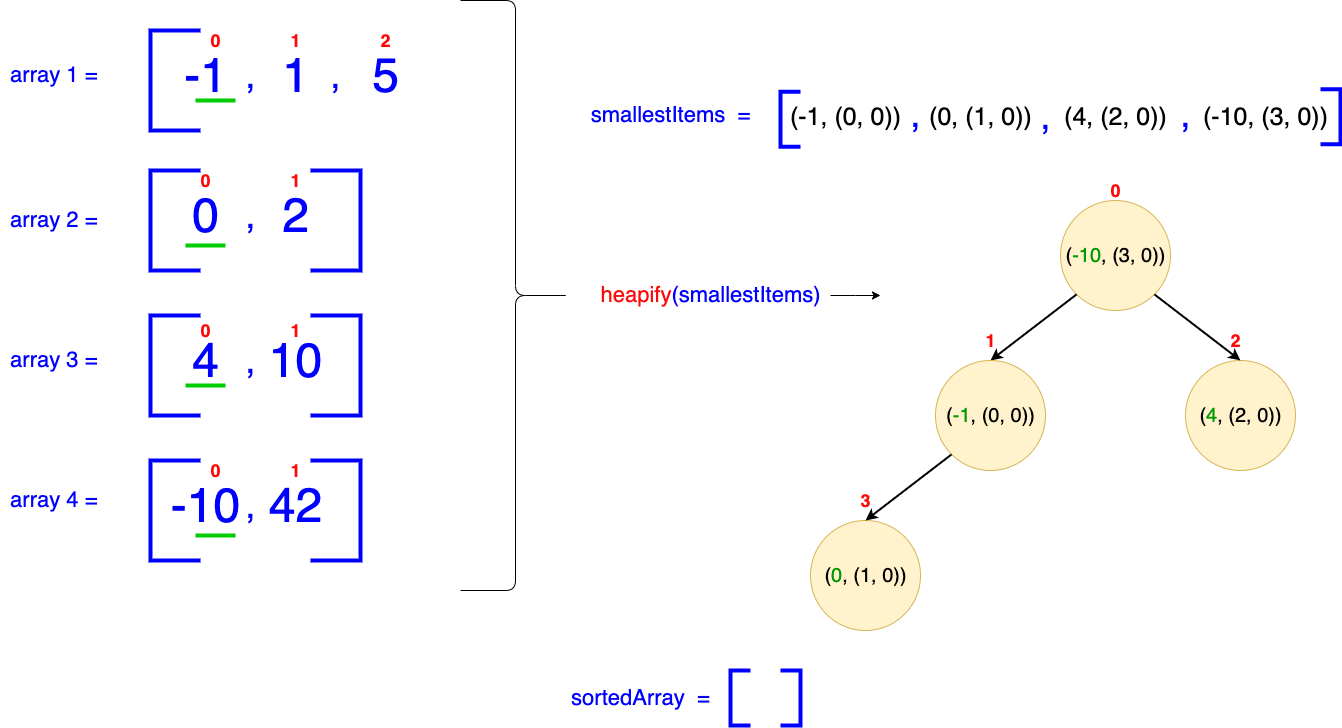
• We start by creating a smallestItems array that will be translated into a MinHeap to efficiently determine the next smallest element among all the arrays.
• Each element in the MinHeap should contain not only the value from the arrays but also information about which array it came from and its index within that array. This is crucial for retrieving the next element from the same array.
• Initially, we populate the MinHeap with the first element of each sorted array (if the array is not empty).
• As we insert each element into the heap, we store it alongside its originating array's index and its index within that array. Since the first element's index is 0 for each array, observe that for each item we have 0 at the end.
• For instance, the first item in the heap (e.g., at idx = 0) is (-10, (3, 0)). Here, -10 is the smallest number among all the arrays, making it the first item in our heap. This integer originates from array-4, which corresponds to the array at idx = 3; thus, the number 3 appears. This number is located at idx = 0 in array-4, as indicated by the second number 0.

Iteration 1

• We know that the root element of our heap (e.g., the first item in our array representing a MinHeap) is the current smallest item. That's why we pop it from the heap and add it to our sortedArray.
• The extracted item is (-10, (3, 0)). This tells us the originating array (e.g., array-4) and the index of the popped integer within that array (e.g., at index = 0). Consequently, we insert the next item from that array into the MinHeap, assuming there are more elements remaining in the array. The next smallest item in that array is 42, located at index = 1 in the array at index = 3.
• So, we insert (42, (3, 1)) into our heap. For a better understanding of how insertion and removal in a MinHeap work, please refer to this resource.

Iteration 2

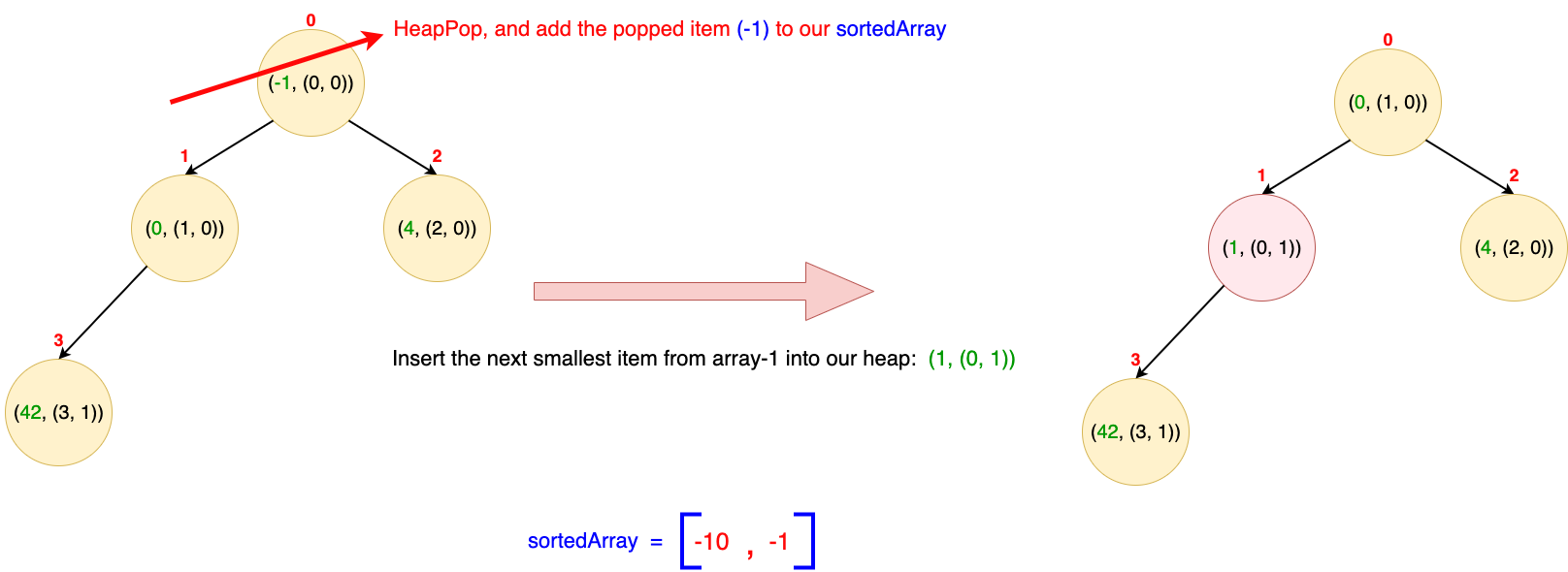
• We know that the root element of our heap is the current smallest item. That's why we pop it from the heap and add it to our sortedArray.
• The extracted item is (-1, (0, 0)). This tells us the originating array (e.g., array-1) and the index of the popped integer within that array (e.g., at index = 0). Consequently, we insert the next item from that array into the MinHeap, assuming there are more elements remaining in the array. The next smallest item in that array is 1, located at index = 1 in the array at index = 0.
• So, we insert (1, (0, 1)) into our heap. Again, for a better understanding of how insertion and removal in a MinHeap work, please refer to this resource.

Iteration 3

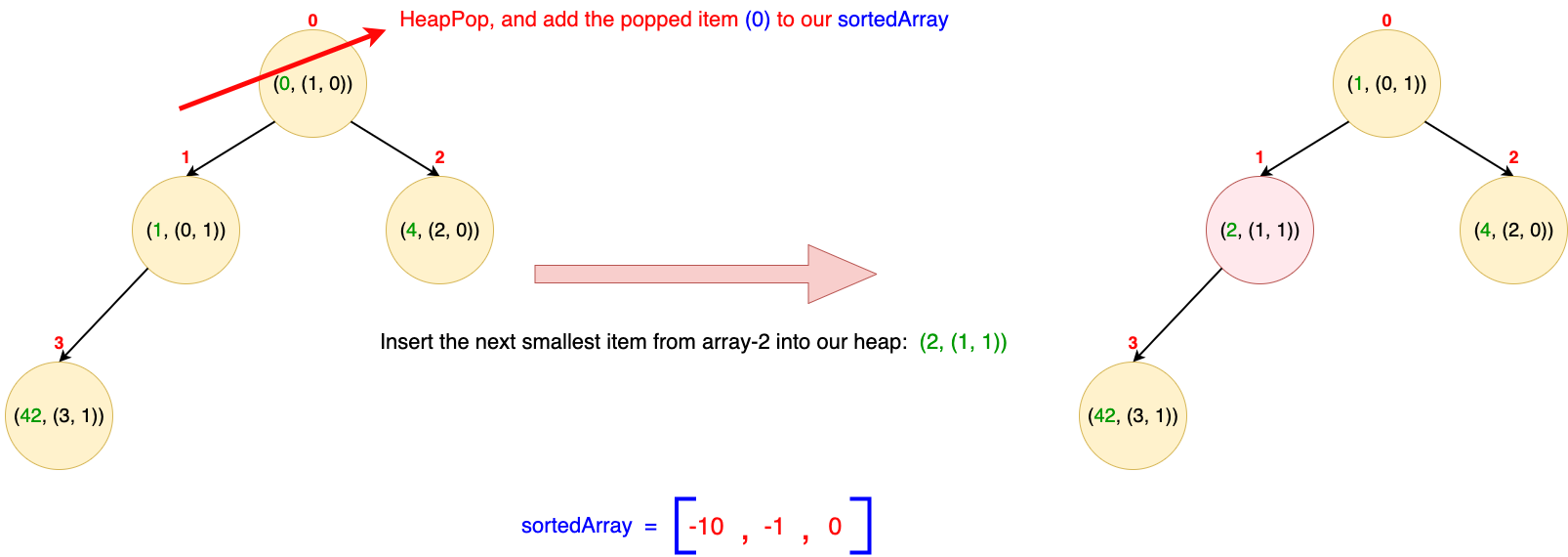
• We know that the root element of our heap is the current smallest item. That's why we pop it from the heap and add it to our sortedArray.
• The extracted item is (0, (1, 0)). This tells us the originating array (e.g., array-2) and the index of the popped integer within that array (e.g., at index = 0). Consequently, we insert the next item from that array into the MinHeap, assuming there are more elements remaining in the array. The next smallest item in that array is 2, located at index = 1 in the array at index = 1.
• So, we insert (2, (1, 1)) into our heap. Again, for a better understanding of how insertion and removal in a MinHeap work, please refer to this resource.

Iteration 4

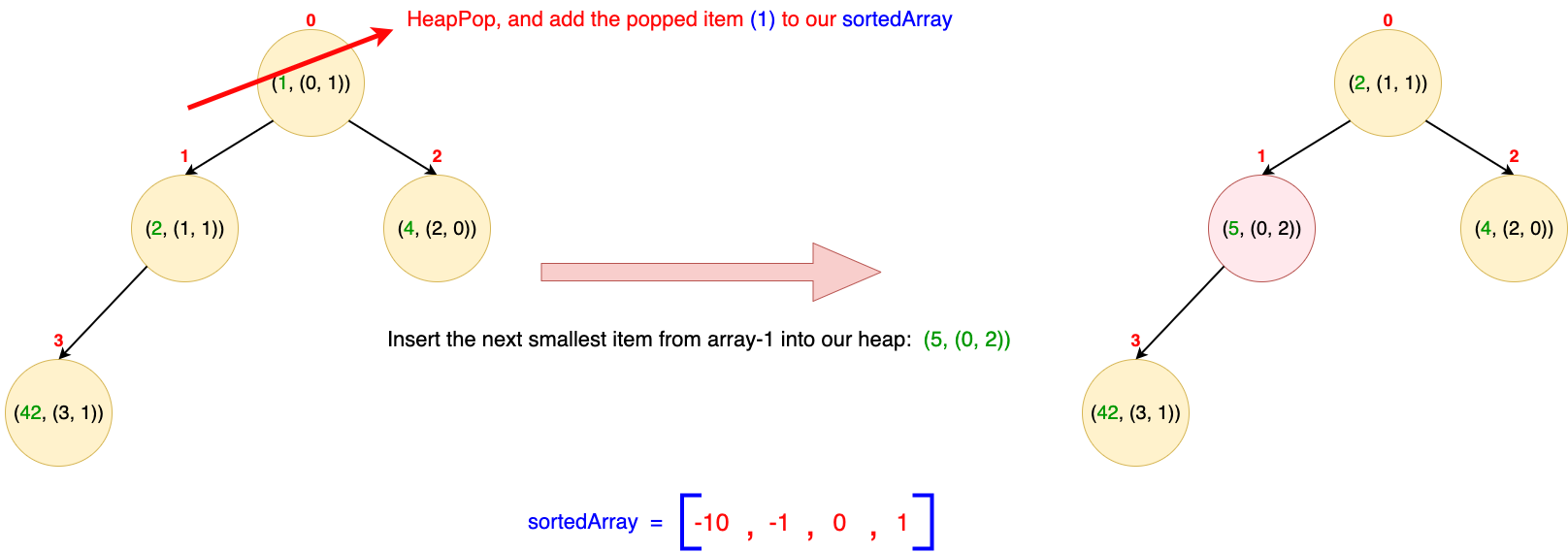
• We know that the root element of our heap is the current smallest item. That's why we pop it from the heap and add it to our sortedArray.
• The extracted item is (1, (0, 1)). This tells us the originating array (e.g., array-1) and the index of the popped integer within that array (e.g., at index = 1). Consequently, we insert the next item from that array into the MinHeap, assuming there are more elements remaining in the array. The next smallest item in that array is 5, located at index = 2 in the array at index = 0.
• So, we insert (5, (0, 2)) into our heap. Again, for a better understanding of how insertion and removal in a MinHeap work, please refer to this resource.

Iteration 5

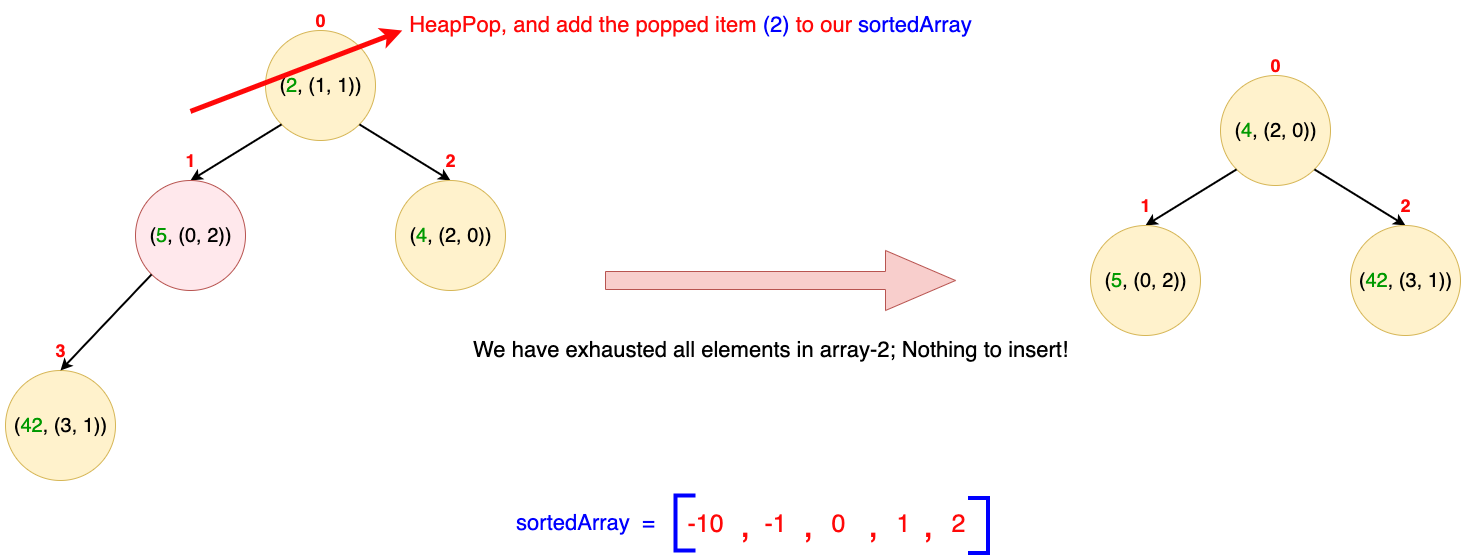
• We know that the root element of our heap is the current smallest item. That's why we pop it from the heap and add it to our sortedArray.
• The extracted item is (2, (1, 1)). This tells us the originating array (e.g., array-2) and the index of the popped integer within that array (e.g., at index = 1). However, there is no next item in array-2 as we have exhausted all its items. Thus, our heap will now have only 3 items in it.

Iteration 6

• We know that the root element of our heap is the current smallest item. That's why we pop it from the heap and add it to our sortedArray.
• The extracted item is (4, (2, 0)). This tells us the originating array (e.g., array-3) and the index of the popped integer within that array (e.g., at index = 0). Consequently, we insert the next item from that array into the MinHeap, assuming there are more elements remaining in the array. The next smallest item in that array is 10, located at index = 1 in the array at index = 2.
• So, we insert (10, (2, 1)) into our heap.

Iteration 7

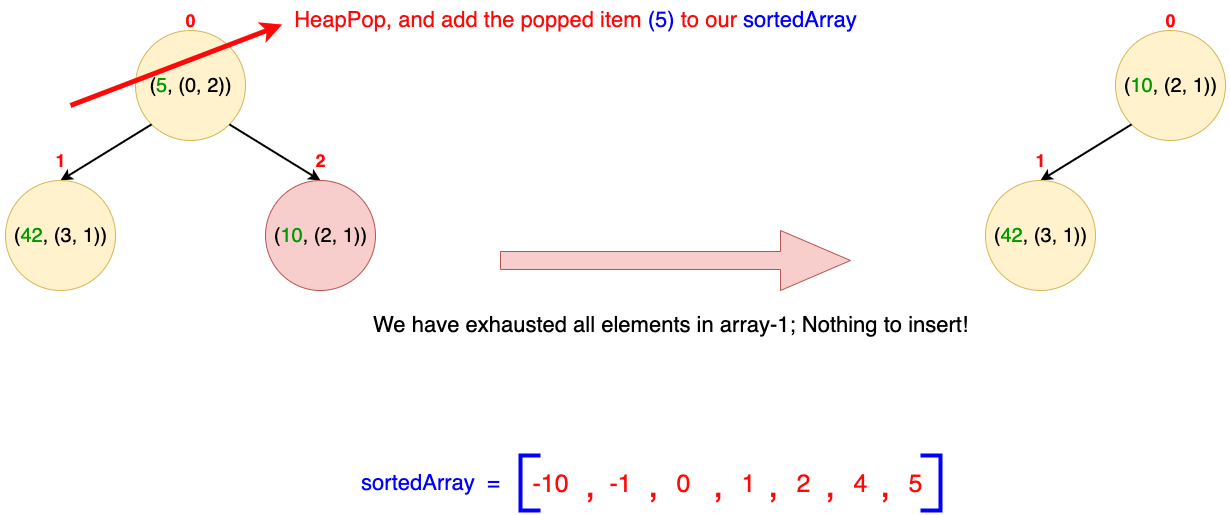
• We know that the root element of our heap is the current smallest item. That's why we pop it from the heap and add it to our sortedArray.
• The extracted item is (5, (0, 2)). This tells us the originating array (e.g., array-1) and the index of the popped integer within that array (e.g., at index = 2). However, there is no next item in array-1 as we have exhausted all its items. Thus, our heap will now have only 2 items in it.

Iteration 8

• We know that the root element of our heap is the current smallest item. That's why we pop it from the heap and add it to our sortedArray.
• The extracted item is (10, (2, 1)). This tells us the originating array (e.g., array-3) and the index of the popped integer within that array (e.g., at index = 1). However, there is no next item in array-3 as we have exhausted all its items. Thus, our heap will now have only 1 item left in it.

Iteration 9 (Final Iteration)

• The root node of our heap is, in fact, the leaf node since we have only one item remaining in our heap. We pop it and add it to our sortedArray.
• The extracted item is (42, (3, 1)). This tells us the originating array (e.g., array-4) and the index of the popped integer within that array (e.g., at index = 1). However, there are no more items left in array-4, indicating that we have exhausted all its items. Consequently, this implies that all items from all input arrays have been processed, leaving us with an empty heap.
• This marks the end of our while loop, indicating that our sortedArray is now complete.

Complexity Analysis

• Time Complexity: O(nlog(k)), where n is the total number of items across all arrays, and k is the number of input arrays.

  Explanation:

  1. Iterating Through Items

     • We iterate through all items to add a total of n items to our final sorted list.

  2. Heap Operations

     • At any given time, our heap will contain at most k items.
     • Popping an item from a heap of size k requires O(log(k)) time.
     • Inserting an item into a heap of size k also requires O(log(k)) time.

  Combining these steps, the overall time complexity is O(nlog(k)), which includes iterating through all items and performing heap operations for each item.

• Space Complexity: O(n + k). The space complexity is mainly influenced by the storage requirements of the sorted array and the heap.

  Explanation:

  1. Final Sorted Array

     • We need to store a total of n items in our final sorted array.

  2. MinHeap

     • The MinHeap array, which has a length of k, is used to track the smallest item in each input array at any given point in time.

  Therefore, the overall space complexity is O(n + k), accommodating the necessary data structures for efficient processing.

Final Notes

Here are some key points and tips to help you ace this question in a Meta interview:

1. Initial Approach: Start by proposing the intuitive solution that concatenates and sorts the arrays. Mention that this has a time complexity of O(nlog(n)), where n is the total number of elements. This demonstrates your understanding of basic problem-solving techniques and gives you a foundation to build upon.

2. Optimal Solution: Transition to discussing the optimal solution using a MinHeap. Explain that the MinHeap allows for efficiently finding the smallest element across multiple sorted arrays, reducing the time complexity to O(nlog(k)), where k is the number of arrays. This shows your ability to optimize solutions and your familiarity with more advanced data structures.

3. Heap Implementation: Be prepared to discuss the implementation of a MinHeap. Interviewers at Meta will likely hint at using a heap and may provide you with an implementation. If not, ask if you can use a built-in data structure like PriorityQueue in Java or heapq in Python. This shows you know how to leverage existing tools to solve problems efficiently.

4. Edge Cases: Always consider edge cases, such as when one or more arrays are empty. Clarify with your interviewer how such cases should be handled, demonstrating thoroughness in your approach.

5. Communication: Clearly articulate your thought process throughout the interview. Explain why you are choosing a particular approach and how you plan to implement it. This not only shows your problem-solving skills but also your ability to communicate complex ideas effectively.

6. Practice: Familiarize yourself with common algorithms and data structures, especially heaps. Practicing problems involving heaps and their operations will make you more comfortable discussing and implementing them during the interview.

7. Time Management: Manage your time wisely during the interview. Start with a simple solution and then move to the more optimal one. This way, you ensure that you at least have a working solution before diving into more complex optimizations.

8. Ask Questions: If something in the problem statement is unclear, don't hesitate to ask for clarification. Understanding the problem correctly is crucial for providing an accurate and efficient solution.

By following these tips and thoroughly understanding the problem and its solutions, you'll be well-prepared to tackle this question in a Meta interview.