Q1 - Meta Social Graph Problem
We believe this interview question has been asked to full-time software engineering candidates applying for various positions at Meta.
At Meta, you're part of the team that's constantly innovating to keep user interactions both meaningful and engaging. The social graph, a vast network of user connections, is at the heart of Meta's platform. It's where friends, family, and various other relationships come to life digitally. The way these connections are presented can significantly impact user engagement.
The project at hand involves creatively restructuring the social graph's linked list representation. The aim is to alter the order of connections in a user's profile to introduce a fresh, dynamic perspective. This new structure, referred to as a "zipped" linked list, interlaces the nodes to balance visibility between recent and less recent connections.
Your task is to write a function that reorders the linked list of user connections, maintaining the original data structure. The reordering of the linked list nodes should be in place (without using any additional data structure). This "zipping" process should bring the head of the list together with the tail, then proceed with the next head and the previous tail, and so on. The function should return the head of the restructured linked list.
The function must transform the linked list in place; it's essential that no new list is created during this process. The reordering of connections should be done within the original list structure, ensuring that the transformation is both space-efficient and maintains the integrity of the original data.
Example 1
Input:
1 -> 2 -> 3 -> 4 -> 5
Output:
1 -> 5 -> 2 -> 4 -> 3
Example 2
Input:
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7
Output:
1 -> 7 -> 2 -> 6 -> 3 -> 5 -> 4
Example 3
Input:
1 -> 2
Output:
1 -> 2
Solution
An initial, straightforward approach to zipping a linked list might involve creating an additional array. We would iterate through the original linked list, adding each node to this extra array. Then, a new linked list would be constructed by adding nodes from the auxiliary array in an alternating pattern (first node from the beginning of the array, and the second node from the end, etc). However, the given problem specifies that the input linked list must be transformed in place, which means we need to avoid using any additional space for storing or rearranging the nodes. This suggests that the space complexity of our solution must be O(1), making this problem a challenging one.
How can we tackle this problem without using any extra space? Well, that's where the 'Zip Linked List' algorithm comes into play. We will cleverly rearrange the input singly linked list by alternating the first half of the list with its reversed second half. The outcome? A 'zipped' version of the original list, where the end elements cozy up to the front, mingling the two halves together. It's pretty neat because it works its magic in-place, so no extra storage needed, and it's efficient, running in O(n) time. Let's dive into how exactly this is done in the following sections:
-
Finding the Middle of the List: Using the two-pointer technique (a slow pointer and a fast pointer), the algorithm locates the middle node of the list. The slow pointer moves one node at a time, while the fast pointer moves two nodes at a time. When the fast pointer reaches the end, the slow pointer is positioned at the midpoint.
-
Reversing the Second Half: Starting from the middle node identified in the previous step, the second half of the list is reversed. This in-place reversal rearranges the nodes so that the last node becomes the start of the second half.
-
Merging the Two Halves: Finally, the algorithm alternates nodes from the first half and the reversed second half. This step involves careful pointer manipulation to ensure that the nodes are rearranged correctly without breaking the list.
In the next section we will go through each step in more detail.
1) Finding the Middle of the List
The objective here is to pinpoint the middle node in our singly linked list. But why the middle? Well, knowing where the middle is helps us divide the list into two halves — necessary for the zipping process later on. To find this midpoint efficiently, we use a classic technique in linked list problems: the two-pointer approach. Here's how it goes in the code:
# Main function.
def zip_linked_list(linked_list):
# Find the middle node in our LinkedList.
slow, fast = linked_list, linked_list
while fast and fast.next:
slow = slow.next
fast = fast.next.next
# At the end of while loop, "slow" node will be the middle node.
...
- Initialization: We start with two pointers,
slowandfast, both initially pointing to the head of the list. - Traversal: On each step,
slowmoves one node forward (slow = slow.next), whilefastmoves two nodes forward (fast = fast.next.next). - Why Two Speeds?: The magic here is in the different speeds. Since
fastmoves twice as fast asslow, by the time fast reaches the end of the list (or gets to the last node in case of an even number of nodes),slowwill be right at the midpoint.
Iteration 0
1 -> 2 -> 3 -> 4 -> 5
S,F
Iteration 1
1 -> 2 -> 3 -> 4 -> 5
S F
Iteration 2
1 -> 2 -> 3 -> 4 -> 5
S F
The iteration ends when either of fast or fast.next are null. In this example, fast.next = None, and we can stop.
You can see that by the end, the slow pointer is indeed the middle node of our input linked list.
This technique works efficiently because it traverses the list only once, hence O(n) time, where n is the number of nodes in the list.
By the time fast has seen every node (twice as fast), slow has only reached the middle, effectively finding the midpoint in one pass.
So, by the end of this part, we've got our list split into two parts (mentally, not physically): the first half, up to (but not including) slow,
and the second half, starting from slow. Next up, we'll see how to reverse this second half and then how to interlace it with the first half to achieve our "zipped" list.
2) Reversing the Second Half
After identifying the middle node, the next crucial step is to reverse the second half of the list. But why do we need to reverse it? The goal is to prepare the list for a seamless zipping process, where we alternate between the nodes from the first and the now-reversed second half. This reversal makes it possible to pull nodes from the end of the list up front in the zipping phase, creating the interleaved effect.
Intuition Behind Reversing: In our zipping process, we aim to bring the last node up against the first node, the second-last against the second, and so on. By reversing the second half of the list, the nodes that were at the end are now positioned to be merged easily with the nodes in the first half. This sets up a pattern where we seamlessly alternate between the two halves.
Let's consider our initial example linked list: 1 -> 2 -> 3 -> 4 -> 5. We've found that the slow (middle) node is 3. The goal now is to reverse the part of the list starting from 3
(e.g., 3 -> 4 -> 5). The diagram below shows the expected outcome of this process:
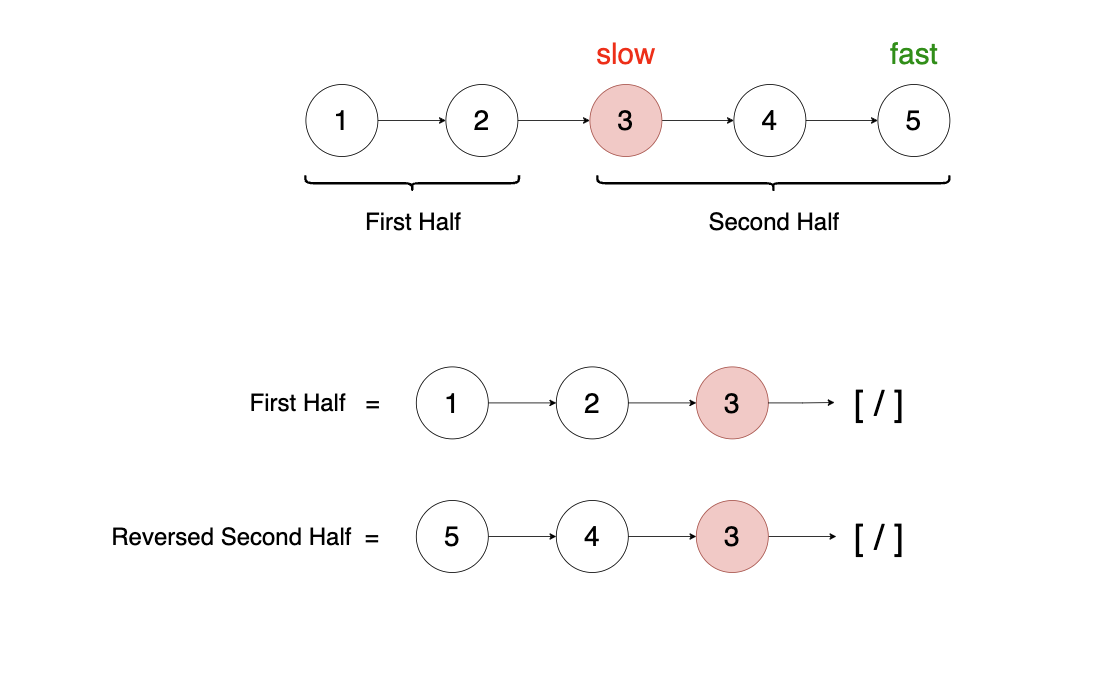
Notice that the node 3 appears in both the first half (1 -> 2 -> 3) and the reversed second half (5 -> 4 -> 3) of the list.
In the next section, we'll see how the code handles this overlap to avoid duplicating 3 in the zipped list.
Below code snippet will reverse the second half of the list to get 5 -> 4 -> 3 -> [/]. Observe that the input is the second half (e.g., slow node, which is 3):
# Main function.
def zip_linked_list(linked_list):
...
# At the end of while loop, "slow" node will be the middle node.
# Reverse the linked list after the middle node (including the mid-node).
# e.g., 1 -> 2 -> 3 -> 4 -> 5 -> 6
# First half: 1 -> 2 -> 3 | Second half: 6 -> 5 -> 4
second_half_reversed = reverse_linked_list(slow)
...
# Helper function to reverse a linked list.
def reverse_linked_list(linked_list):
prev_node = None
curr_node = linked_list
while curr_node:
next_node = curr_node.next
curr_node.next = prev_node
prev_node = curr_node
curr_node = next_node
return prev_node # Last node of the original linked list.
The list is now prepped for zipping. The reversed second half allows us to interleave its nodes starting from what used to be the last node (5), followed by 4,
and so on, with the nodes in the first half. This reordering creates the alternating pattern characteristic of the "zipped" list, aligning with our goal of reorganizing
the original list in an intertwined fashion.
3) Merging the Two Halves
The final phase of the algorithm involves merging the first half of the list with the reversed second half. This process is where the list gets its "zipped" appearance, intertwining the nodes from each half. The diagram below shows the process of intertwining the nodes from each half:
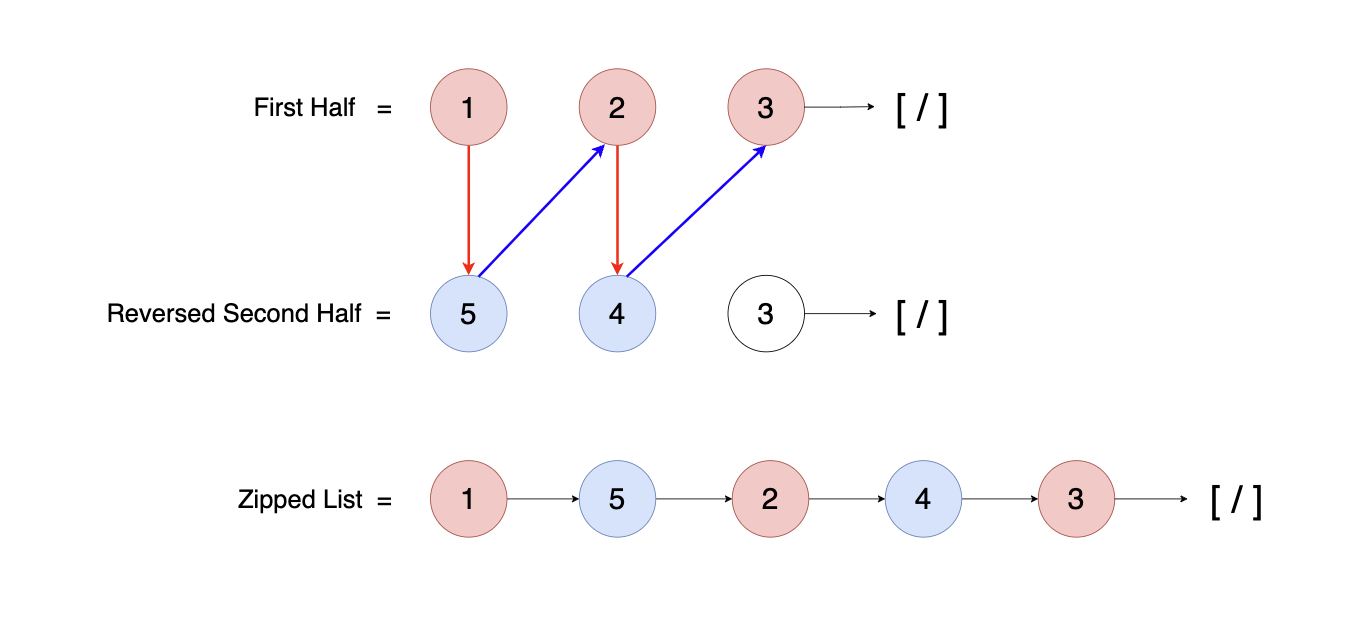
Observe that we are stitching the nodes from the first and second halves together in an alternating pattern. This way, the first node from the first half is followed by the first node from the reversed second half, then the second node from the first half, and so on. Below code snippet forms the zipped linked list:
prehead = LinkedList(-1)
curr = prehead
first_half = linked_list
is_iter_one = True # Decide from which linked list to get the node.
while first_half and second_half_reversed:
# Point to the first half's current node.
if is_iter_one:
curr.next = first_half
first_half = first_half.next
# Point to the second half's current node.
else:
curr.next = second_half_reversed
second_half_reversed = second_half_reversed.next
curr = curr.next
# Flip the flag, so we consider the other part at each iteration.
is_iter_one = not is_iter_one
return prehead.next
In the zipping process, both the first half and the reversed second half initially include the middle node 3.
As we alternate nodes during merging, we pull nodes from each half only as long as both halves have nodes remaining.
Once we exhaust the first half, the loop terminates before we have a chance to duplicate the middle node from the second half.
This way, the shared middle node naturally becomes the last node in the zipped list, ensuring it isn't duplicated.
- Setting Up a Placeholder Node
- We start with a dummy or placeholder node (
prehead). This node doesn't hold any meaningful data but serves as an anchor point for the new zipped list.
- Alternating Between Halves
- We initialize a flag (
is_iter_one) that helps us alternate between appending nodes from the first half and the second half. - We iterate over both halves simultaneously, attaching one node from the first half and then one from the second half to the growing zipped list.
- Handling Node Transitions
- The choice of which half to take the next node from is determined by our alternating flag. Each iteration switches the flag, ensuring the next node comes from the other half.
- We continue this process until we reach the end of one or both halves.
Complexity Analysis
-
Time Complexity: O(n), where n represents the number of nodes in our linked list.
Explanation:
-
Finding the Middle of the List
- This step involves iterating through the list with two pointers (
slowandfast), wherefastmoves at double the speed ofslow. The time complexity for this part is O(n/2), which simplifies to O(n), as constants are dropped in Big O notation.
- This step involves iterating through the list with two pointers (
-
Reversing the Second Half
- Reversing a list involves a single pass from the middle to the end. For a list of n elements, this operation is, in the worst case, another O(n/2) process. Hence, it's an O(n) operation.
-
Merging the Two Halves
- The final step is merging the two halves, which again requires traversing each node once. Despite the alternating process, each node is visited exactly once, resulting in O(n).
Combining these steps, each with a linear time complexity, the overall time complexity of the algorithm remains O(n).
-
-
Space Complexity: O(1): Algorithm operates in place. It does not require any additional space proportional to the input size. All operations are performed by rearranging the existing nodes without allocating any new nodes or data structures. Implementing the algorithm within the constraints of constant space is precisely what adds complexity to this problem. It's a challenge that tests not only our understanding of linked list operations but also our ability to optimize for space efficiency.
Below is the coding solution for the algorithm we've just explored:
class LinkedList:
def __init__(self, value):
self.value = value
self.next = None
# O(n) time | O(1) space
def zip_linked_list(linked_list):
# Find the middle node in our LinkedList.
slow, fast = linked_list, linked_list
while fast and fast.next:
slow = slow.next
fast = fast.next.next
# At the end of while loop, "slow" node will be the middle node.
# Reverse the linked list after the middle node (including the mid-node).
# e.g., 1 -> 2 -> 3 -> 4 -> 5 -> 6
# First half: 1 -> 2 -> 3 | Second half: 6 -> 5 -> 4
second_half_reversed = reverse_linked_list(slow)
prehead = LinkedList(-1)
curr = prehead
first_half = linked_list
is_iter_one = True # Decide from which linked list to get the node.
while first_half and second_half_reversed:
# Point to the first half's current node.
if is_iter_one:
curr.next = first_half
first_half = first_half.next
# Point to the second half's current node.
else:
curr.next = second_half_reversed
second_half_reversed = second_half_reversed.next
curr = curr.next
# Flip the flag, so we consider the other part at each iteration.
is_iter_one = not is_iter_one
return prehead.next
# O(n) time | O(1) space
# Helper function to reverse a linked list.
def reverse_linked_list(linked_list):
prev_node = None
curr_node = linked_list
while curr_node:
next_node = curr_node.next
curr_node.next = prev_node
prev_node = curr_node
curr_node = next_node
return prev_node # Last node of the original linked list.
Final Notes
We believe this question has been asked frequently by Meta, making it a hot topic for any candidate preparing for an interview with the company.
The Meta Social Graph problem not only tests your ability as a Software Engineer to manipulate data structures but also your ability to enhance user experience
and engagement within a platform as dynamic as Meta. It simulates a real-world challenge that goes beyond simple coding
abilities—it tests your ingenuity and
your ability to work within given constraints while still driving significant change.
Your task of restructuring the social graph's linked list mirrors the kind of problem-solving that is central to Meta's mission—finding novel ways to display and engage with user connections. The zipped linked list is more than just a shuffled set of data; it represents a refreshed, more balanced way for users to view and interact with their network. This approach can lead to more meaningful engagements on the platform.
By maintaining the integrity of the existing data structure and avoiding additional memory allocation, you are essentially being asked to do more with less. This is a common theme in tech companies today, where efficiency and performance optimization are key.
Here are some critical points to keep in mind as you approach this and similar problems:
1. In-Place Transformation: The in-place requirement underscores the importance of efficient memory usage, which is vital in systems that handle a large volume of data, as is the case with social networks like Meta.
2. User Engagement: The alternating node pattern of the "zipped" list ensures that user connections are represented fairly, enhancing the user's experience on the platform. You need to show your passion and understanding of how user engagement drives the core functionality of social platforms. It's about demonstrating your willingness to delve into the user's perspective and iterate on a solution that not only improves the back-end mechanics but also enriches the front-end experience.
This is how you can differentiate from other candidates with strong technical backgrounds. By demonstrating not just a mastery of algorithms and data structures, but also a clear understanding of how your work impacts user experience, you embody the full spectrum of engineering excellence.
3. Algorithm Complexity: Demonstrating an understanding of time and space complexity is crucial. Your ability to develop an O(n) solution with O(1) space complexity shows mastery over both algorithm efficiency and resource management.
4. Problem Solving within Constraints: Meta values engineers who can work within the constraints of an existing system and find creative solutions without needing to overhaul the entire structure.
5. Impact on User Experience: Any solution you implement will directly impact user experience. It's essential to align your technical decisions with the overarching goal of enhancing user interactions on the platform.
6. Understanding of Meta's Core Functions: A deep understanding of the social graph and its significance in a user's social experience on Meta will guide you to more intuitive solutions that are in line with the company's objectives.
7. Communication Skills: Articulating your thought process and solution in a way that non-technical stakeholders can understand is as important as the technical solution itself. It demonstrates that you can bridge the gap between technical and non-technical worlds.
As you prepare for your interviews or delve into the problem-solving process, remember that your technical prowess, combined with your understanding of user experience and efficiency, will not only serve you well at Meta but will also be a testament to your ability to tackle complex problems in any modern tech environment. Keep innovating and optimizing, just as Meta does.

