Q1 - Model Z Assembly Optimization Challenge

Imagine you're a Software Engineer at Tesla, at the forefront of innovating the assembly process for the latest release: the Tesla Model Z. Tesla prides itself on cutting-edge technology not just in its vehicles, but also in the manufacturing process that combines precision and efficiency.

Your challenge is to streamline the assembly line specifically designed for the Model Z. This line is unique, composed of several advanced workstations, each capable of handling multiple tasks, from the intricate battery cell arrangement to the sophisticated autopilot calibration. However, the rate of vehicle production is bottlenecked by the slowest operation in the sequence. Consider a hypothetical assembly line for the Model Z consisting of 50 workstations and 50 tasks, where 49 tasks each take 5 minutes, but one critical task—perhaps the calibration of the advanced autopilot system—takes 10 hours. In this scenario, even with the most efficient distribution of tasks, the best possible outcome for the assembly line would still be dictated by this one task, resulting in a minimum operational time of 10 hours for the workstation handling it.

You're provided with an array, taskDurations, where each element is the time in minutes required for tasks such as installing the new high-density battery pack, programming the neural network for the autopilot, or completing the ultra-resistant paint job. Alongside this, you have numWorkstations, the number of high-tech workstations deployed in this part of the factory.

Your task is to implement a function that orchestrates the Model Z's assembly steps among the available workstations to minimize the maximum time taken by any single workstation. This function should return the longest single-station operation time after optimization.

To clarify, each workstation can handle a set of consecutive tasks (for example, tasks 1, 2, and 3, or tasks 4 and 5), but cannot work on them simultaneously—it must complete one before starting the next. Additionally, the tasks assigned to a workstation must be contiguous in the sequence they appear in the taskDurations array; a workstation cannot skip tasks or select them randomly.

taskDurations: [25, 15, 30, 45, 35, 20]
numWorkStations: 3
Output: 70

Explanation:
Workstation 1: Tasks 0, 1, 2 --> 25 + 15 + 30 = 70 minutes.
Workstation 2: Task 3 --> 45 minutes.
Workstation 3: Tasks 4, 5 --> 35 + 20 = 55 minutes.

Hence, after optimizing Tesla's assembly line, the longest duration of a single workstation 
is 70 minutes. This also suggests that the shortest time required to finish all tasks is 70 minutes.

taskDurations: [25, 15, 30, 45, 35, 20]
numWorkStations: 4
Output: 55

Explanation:
Workstation 1: Tasks 0, 1 --> 25 + 15 = 40 minutes.
Workstation 2: Task 2 --> 30 minutes.
Workstation 3: Task 3 --> 45 minutes.
Workstation 4: Tasks 4, 5 --> 55 minutes.

This example has the same taskDurations as the first one, but it has an additional workstation.
After optimizing Tesla's assembly line, the longest duration of a single workstation is 55 minutes.

Brute Force Approach Intuition

What category do you think this question fits into? What is the objective here? At first glance, it might not be immediately apparent, but this is actually a searching problem. So, how should we tackle this question? Let's start by considering the brute force approach. Discussing the brute force method first is beneficial before diving into a more sophisticated solution. It's also an opportunity to demonstrate your analytical thinking to interviewers, who will appreciate understanding your thought process. The first critical observation we need to make is this: While it's technically possible to evaluate all potential combinations of task allocations across the workstations and select the most efficient one, this approach would be highly inefficient (no pun intended).

First of all, what is the optimal output to this problem? What is the shortest duration in which all workstations can complete their assigned tasks? Essentially, this boils down to asking, "What is the minimum amount of time required for the workstation with the largest workload to complete all its tasks?" When you think about it, this optimal value is in fact bounded by two values:

Lower Bound:    max(taskDurations)

• The lower bound is the maximum value in the taskDurations array. This is because, in the best-case scenario, where workload distribution is perfectly balanced, the most time-consuming task still needs to be completed.
• No matter how you distribute the tasks, one workstation will have to handle the longest task. Therefore, the minimum time any single workstation can take cannot be less than the time required for the longest task.

Upper Bound:    sum(taskDurations)

• The upper bound is the sum of all the values in the taskDurations array. This represents the scenario where one workstation does all the work.
• In the worst-case scenario, if all tasks were assigned to a single workstation, it would take the total sum of all task durations to complete them.
• This is the absolute maximum time it would take for the most burdened workstation to finish, as it's not possible for any workstation to take longer than the time it would take to complete all tasks sequentially.

Given our knowledge of the lower and upper bounds, how would we implement the brute force approach? Take, for instance, Example-1, where taskDurations = [25, 15, 30, 45, 35, 20] and numWorkStations = 3. In this array, the maximum single task duration, which forms our lower bound, is 45, and the sum of all task durations, our upper bound, is 170.

In the brute force method, we iterate through all possible values within the range 45 ≤ x ≤ 170, where x represents a potential optimal maximum duration for a workstation. Below is a demonstration:

When x = 45 (Lower Bound):

• We attempt to distribute tasks without exceeding 45 minutes per workstation.
• However, the task with a duration of 45 minutes itself occupies an entire workstation.
• The remaining tasks [25, 15, 30, 35, 20] cannot be distributed among just two workstations without exceeding 45 minutes on one of them.
• Thus, a distribution that satisfies the condition at x = 45 is not feasible.

When x = 46:

• Here, we slightly increase the maximum duration per workstation.
• Again, one workstation is dedicated to the 45-minute task.
• We try to fit the remaining tasks [25, 15, 30, 35, 20] into two workstations, each having a limit of 46 minutes.
• However, no combination of these tasks can be distributed to two workstations without one of them exceeding 46 minutes.
• For example, the closest distribution [25, 15, 30] and [35, 20] still results in 70 minutes for the first workstation, exceeding our 46-minute limit.
• Therefore, x = 46 also fails to provide a feasible solution.

When x = 69:

• Here, we're testing if the tasks can be distributed among the workstations such that no workstation exceeds 69 minutes.
• One workstation will inevitably take the 45-minute task.
• The challenge is to fit the remaining tasks [25, 15, 30, 35, 20] into two workstations with a 69-minute limit each.
• However, we quickly find that this distribution is not feasible. For instance:
  • If we allocate [25, 15, 30] to one workstation, it sums up to 70 minutes, exceeding our limit of 69 minutes.
  • Any other distribution of these tasks also results in one of the workstations exceeding the 69-minute limit.
• Consequently, x = 69 fails to provide a feasible solution.

When x = 70:

• Now, we increase the limit slightly to 70 minutes per workstation.
• Again, one workstation handles the 45-minute task.
• This time, the remaining tasks [25, 15, 30, 35, 20] need to fit into two workstations, each with a 70-minute limit.
• A feasible distribution is found:
  • One workstation takes [25, 15, 30], totaling exactly 70 minutes.
  • The other workstation takes [35, 20], totaling 55 minutes.
• This distribution successfully allocates tasks within the 70-minute limit per workstation.
• Therefore, x = 70 is the first value that allows for a feasible distribution of tasks.

Complexity Analysis of Brute-Force Approach:

• Time Complexity: O(N*M), where N represents the number of tasks (or durations) in the list and M represents the sum of all task durations, the number of potential maximum durations to check is proportional to M. (e.g., technically the range we are looking for is sum(taskDurations) - max(taskDurations), but we take the upper bound in our complexity analysis, thus M = sum(taskDurations)).

  Explanation:
  1. Iterating Through Possible Durations
     • The approach involves iterating through potential maximum durations for a workstation, ranging from the maximum task duration to the sum of all task durations.
     • If M represents the sum of all task durations, the number of potential maximum durations to check is proportional to M.
  2. Checking Feasibility for Each Duration
     • For each candidate duration, we need to assess whether it's possible to distribute all tasks within this limit.
     • This assessment involves trying different combinations of contiguous tasks to see if they fit within the candidate duration without exceeding it.
     • The process of checking each combination involves iterating through the taskDurations array, which has N elements resulting in O(N) time complexity in each iteration.
     • Hence, O(N*M) time complexity in total.

• Space Complexity: O(1). Our solution does not require additional space; all operations are performed in-place.
  

This approach seems promising, right? Even our brute force method uses an interval, but it's important to recognize that this isn't the most efficient solution. It becomes evident that iterating through every possible candidate value within the range max(taskDurations) ≤ optimal_solution ≤ sum(taskDurations) isn't necessary. As we've identified earlier, this challenge is fundamentally a searching problem. Consequently, it should be approached as such. This realization leads us to an important question: Shouldn't we consider employing Binary Search to find the optimal solution more efficiently?

This is because the potential optimal solutions (maximum durations for a workstation) inherently follow a sorted order. If a certain maximum duration is feasible, any larger duration will also be feasible. This ordered nature is a fundamental requirement for binary search. Thus, we can efficiently narrow down the range of potential solutions. Instead of checking every possible maximum duration between the minimum and maximum bounds, binary search splits this range and checks the middle value. For each duration checked during binary search, we can quickly determine whether it's a feasible maximum duration by trying to distribute the tasks among the workstations without exceeding this duration. This check is relatively efficient and aligns well with the binary search process.

Solution with Binary Search (Optimal)

We will go through Example-1 to provide a better intuition to our readers. The following walkthrough is aligned with the algorithm used in our solution.

taskDurations: [25, 15, 30, 45, 35, 20]
numWorkStations: 3
Output: 70

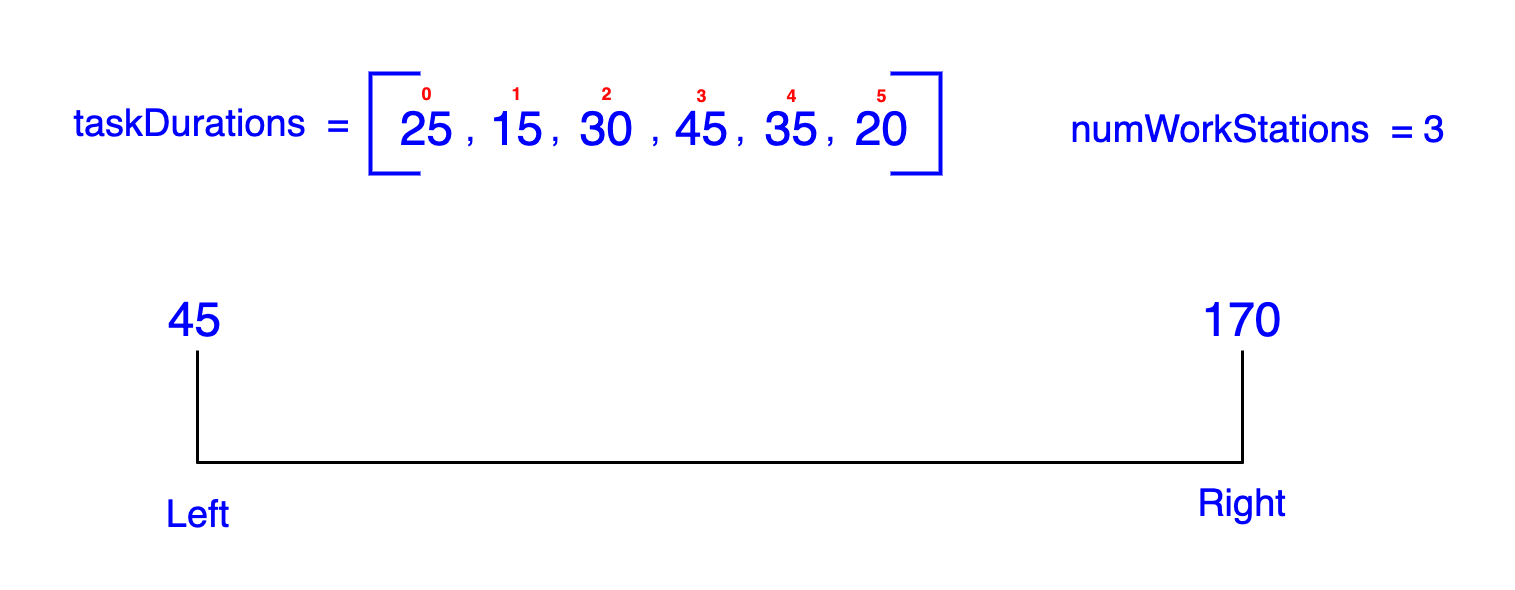
Iteration 1:

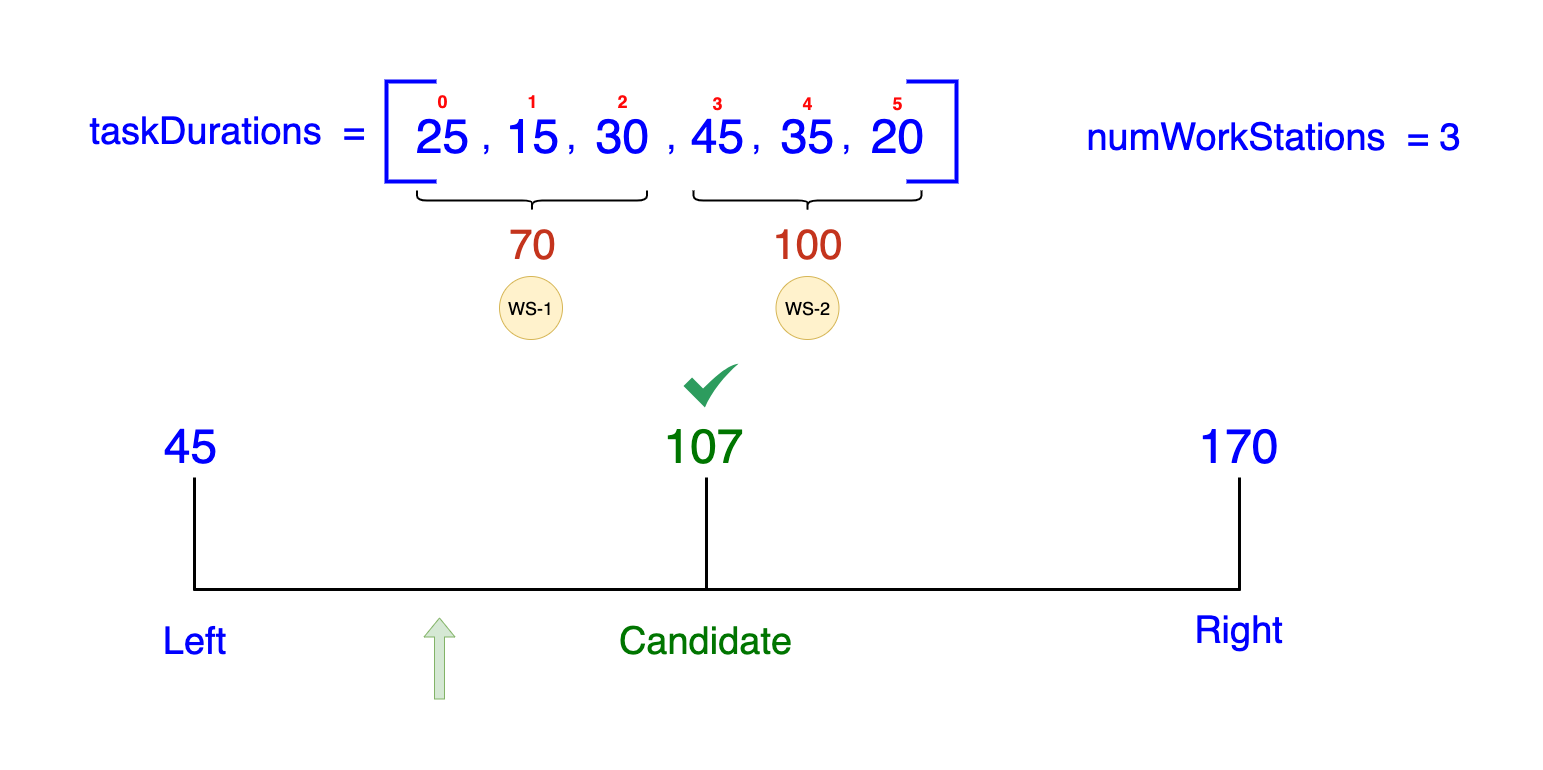
• Midpoint: (45 + 170) / 2 = 107.5  (rounded down to 107)
• Check if a distribution with a maximum of 107 minutes per station is feasible:
  • Workstation 1: [25, 15, 30]  (Total = 70, fits within 107)
  • Workstation 2: [45, 35, 20]  (Total = 100, fits within 107)
  • Workstation 3: We did not even need the Workstation 3 to achieve this solution!
• Result: Feasible
• Action: Move the  Right  pointer to  107 - 1 = 106  (since we know we can do better than 107).

Iteration 2:

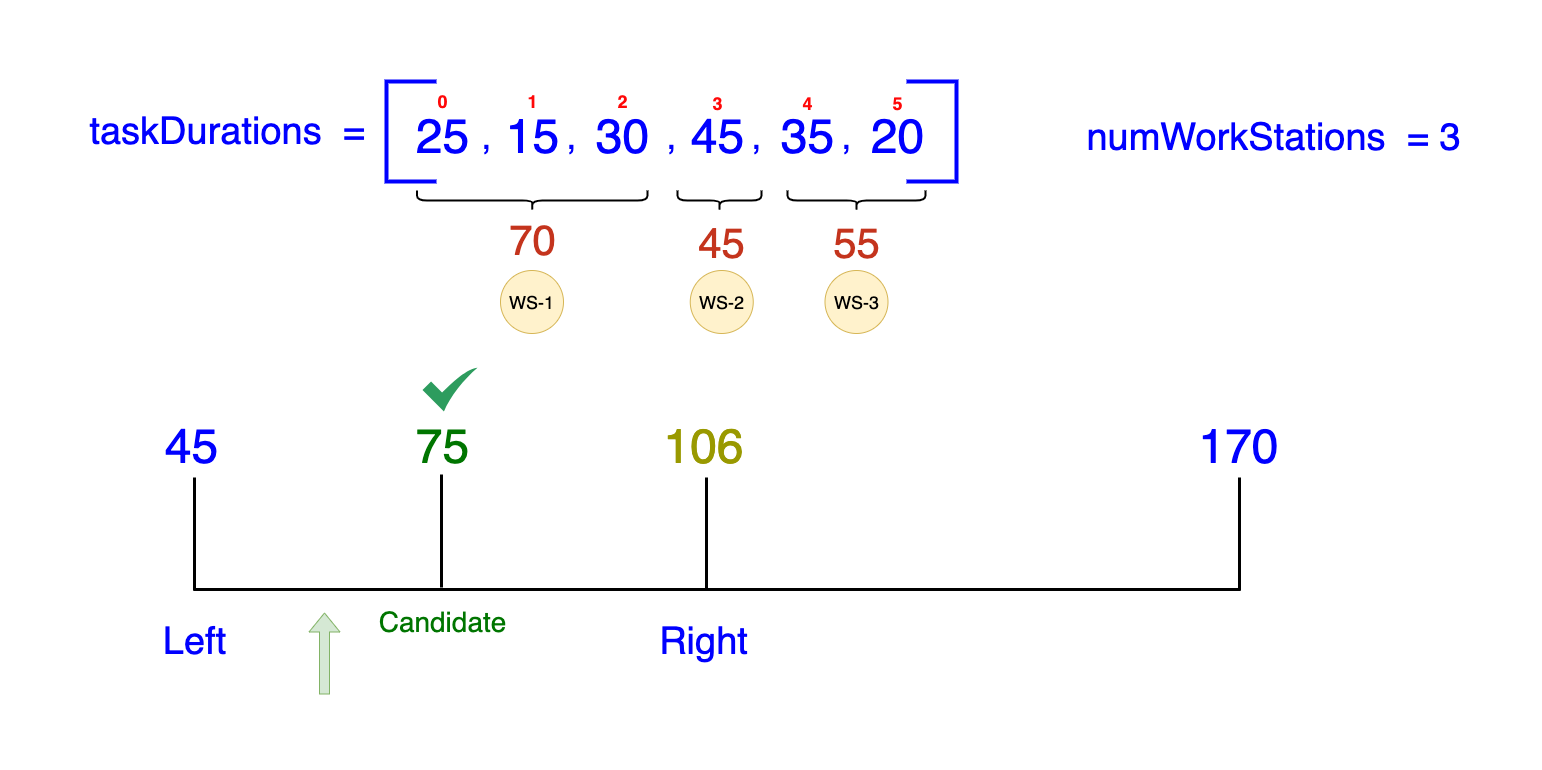
• Midpoint: (45 + 106) / 2 = 75.5  (rounded down to 75)
• Check if a distribution with a maximum of 75 minutes per station is feasible:
  • Workstation 1: [25, 15, 30]  (Total = 70, fits within 75)
  • Workstation 2: [45]  (Total = 45, fits within 75)
  • Workstation 3: [35, 20]  (Total = 55, fits within 75)
• Result: Feasible
• Action: Move the  Right  pointer to  75 - 1 = 74  (since we know we can do better than 75).

Iteration 3:

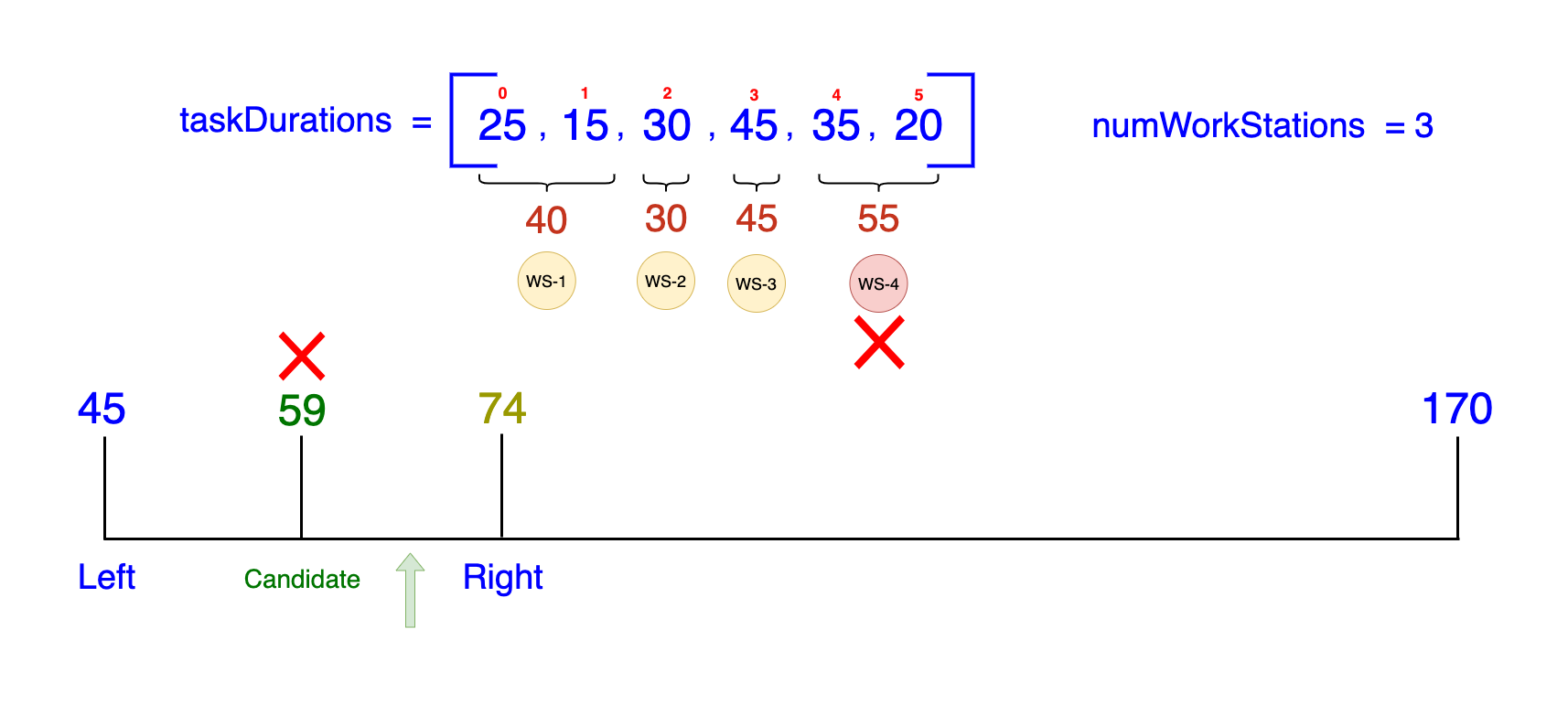
• Midpoint: (45 + 74) / 2 = 59.5  (rounded down to 59)
• Check if a distribution with a maximum of 59 minutes per station is feasible:
  • Workstation 1: [25, 15]  (Total = 40, fits within 59)
  • Workstation 2: [30]  (Total = 30, fits within 59)
  • Workstation 3: [45]  (Total = 45, fits within 59)
  • Missing Tasks: A Fourth Workstation is needed for the remaining tasks  [35, 20]  ❌

• Result: Not Feasible
• Action: Move the  Left  pointer to  59 + 1 = 60  (since we know we cannot achieve 59 or smaller durations).

Iteration 4:

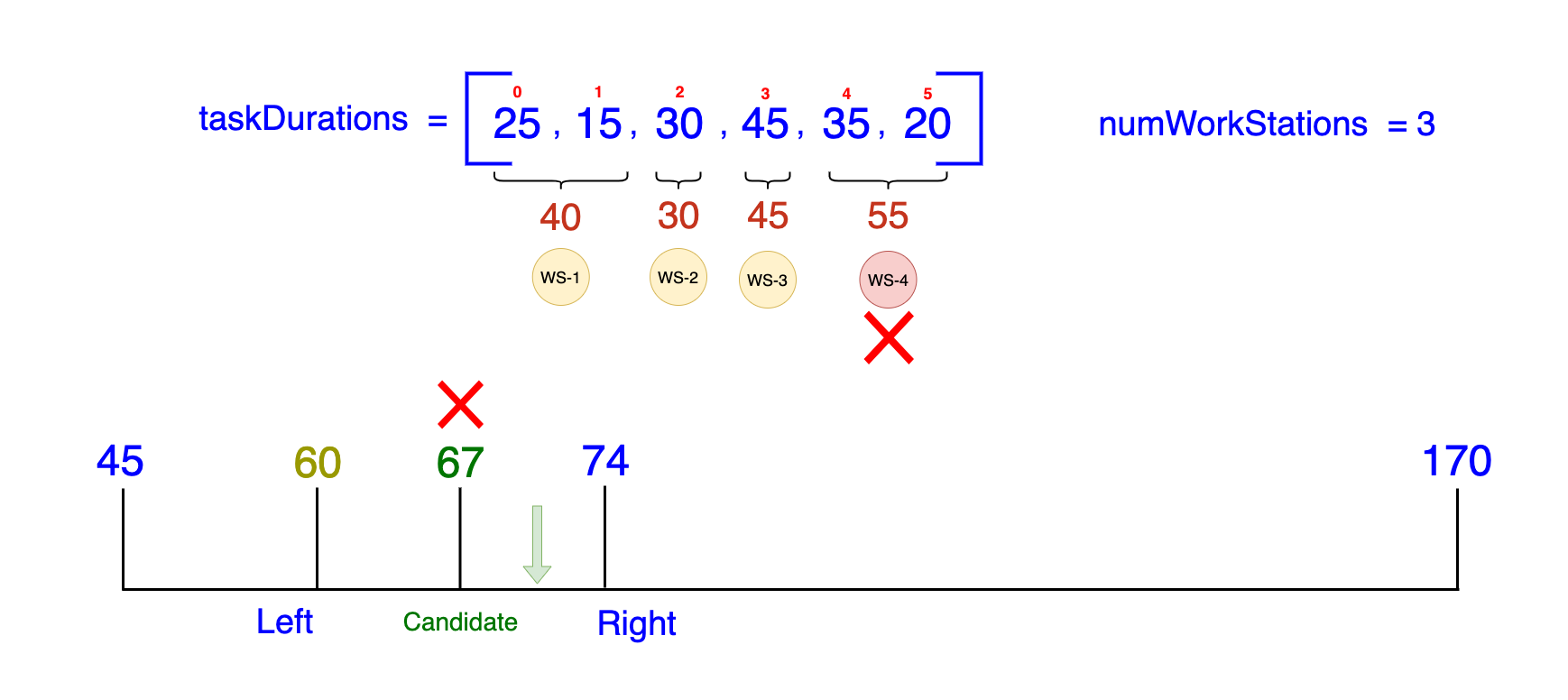
• Midpoint: (60 + 74) / 2 = 67
• Check if a distribution with a maximum of 67 minutes per station is feasible:
  • Workstation 1: [25, 15]  (Total = 40, fits within 67)
  • Workstation 2: [30]  (Total = 30, fits within 67)
  • Workstation 3: [45]  (Total = 45, fits within 67)
  • Missing Tasks: A Fourth Workstation is needed for the remaining tasks  [35, 20]  ❌

• Result: Not Feasible
• Action: Move the  Left  pointer to  67 + 1 = 68  (since we know we cannot achieve 67 or smaller durations).

Iteration 5:

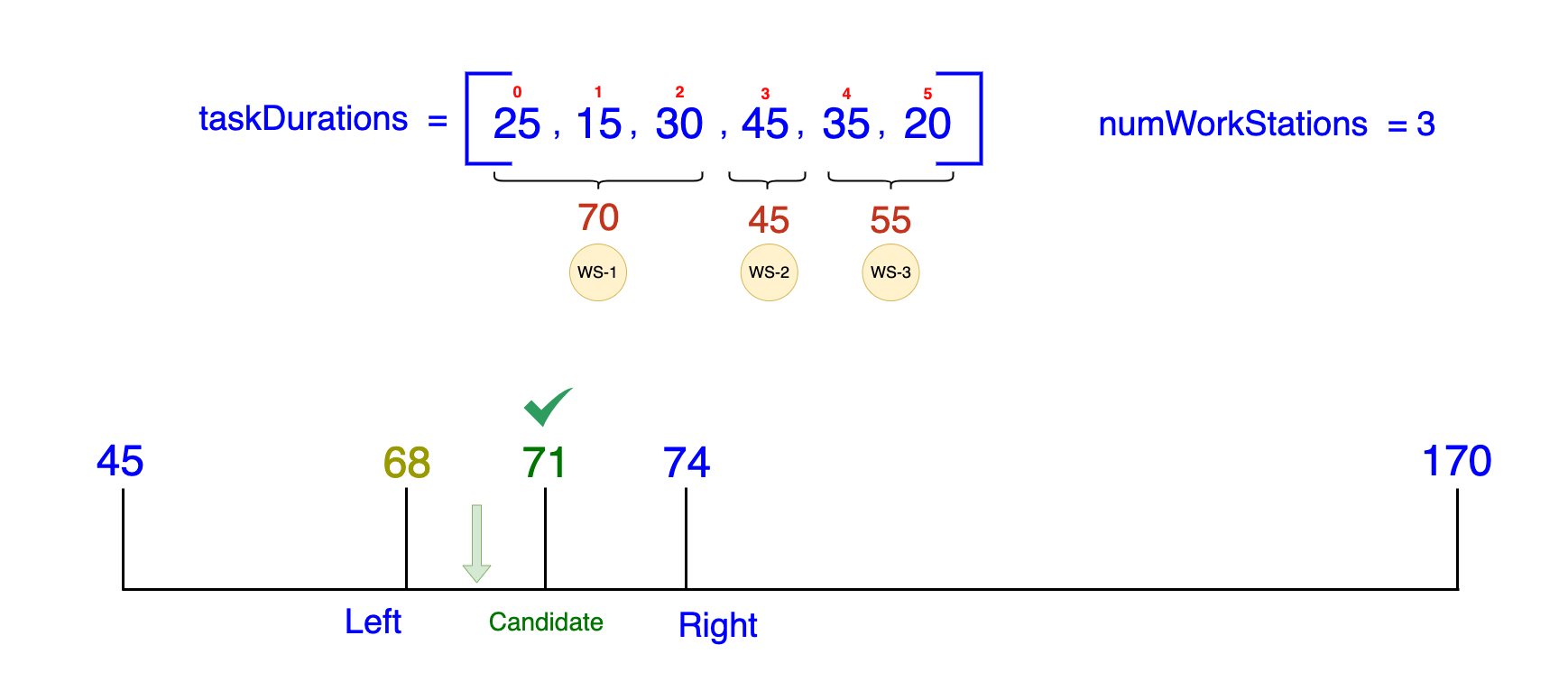
• Midpoint: (68 + 74) / 2 = 71
• Check if a distribution with a maximum of 71 minutes per station is feasible:
  • Workstation 1: [25, 15, 30]  (Total = 70, fits within 71)
  • Workstation 2: [45]  (Total = 45, fits within 71)
  • Workstation 3: [35, 20]  (Total = 55, fits within 71)
• Result: Feasible
• Action: Move the  Right  pointer to  71 - 1 = 70  (since we know we can do better than 71).

Iteration 6:

• Midpoint: (68 + 70) / 2 = 69
• Check if a distribution with a maximum of 69 minutes per station is feasible:
  • Workstation 1: [25, 15]  (Total = 40, fits within 69)
  • Workstation 2: [30]  (Total = 30, fits within 69)
  • Workstation 3: [45]  (Total = 45, fits within 69)
  • Missing Tasks: A Fourth Workstation is needed for the remaining tasks  [35, 20]  ❌

• Result: Not Feasible
• Action: Move the  Left  pointer to  69 + 1 = 70  (since we know we cannot achieve 69 or smaller durations).

Iteration 7 (Last iteration where Left = Right = 70):

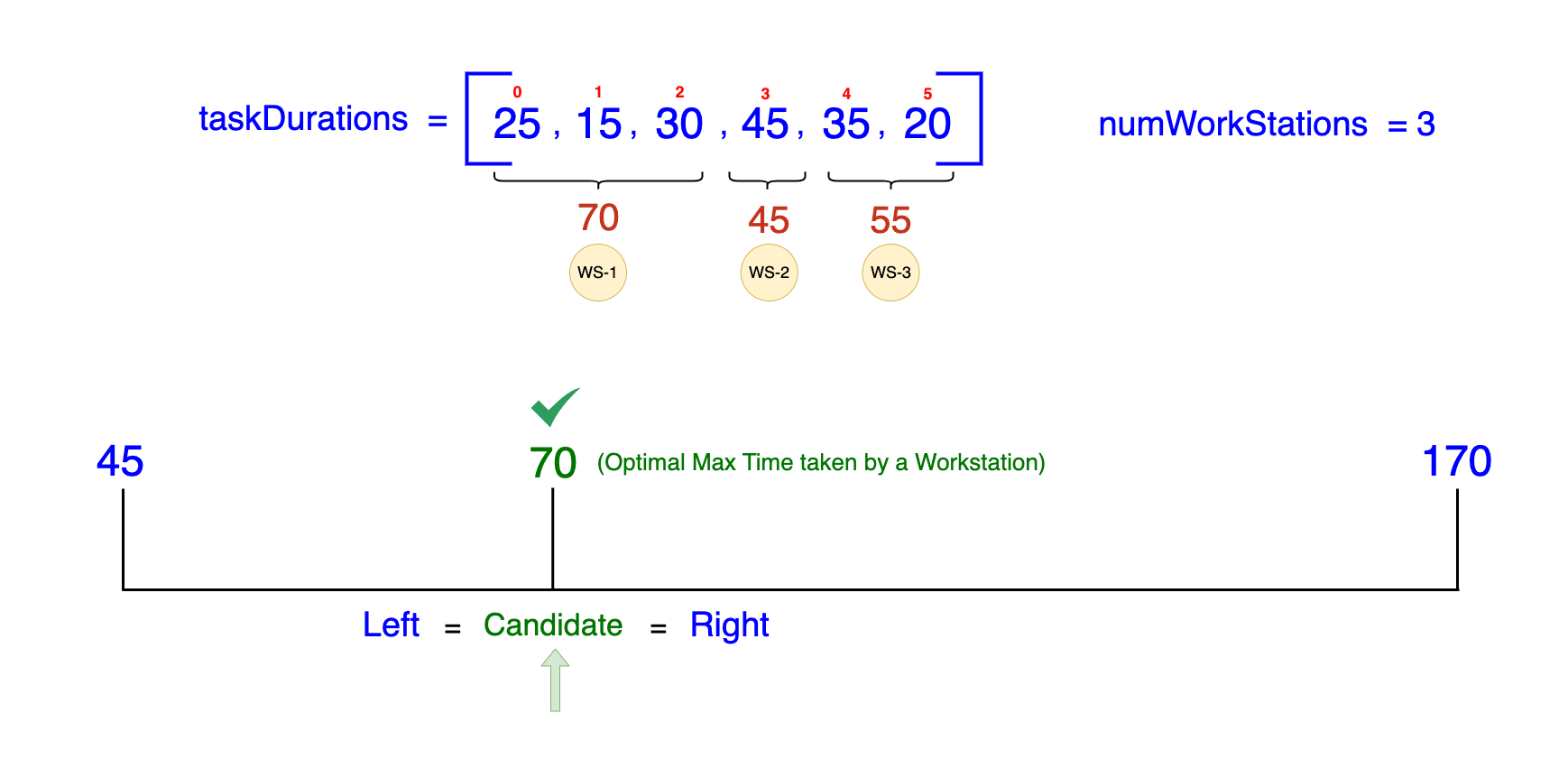
• Midpoint: (70 + 70) / 2 = 70
• Check if a distribution with a maximum of 70 minutes per station is feasible:
  • Workstation 1: [25, 15, 30]  (Total = 70, exactly 70)
  • Workstation 2: [45]  (Total = 45, fits within 70)
  • Workstation 3: [35, 20]  (Total = 55, fits within 70)
• Result: Feasible (optimal solution)
• Action: The convergence of our  Left  and  Right  pointers at a duration of 70 indicates that this is the best possible outcome. Therefore, the optimal maximum duration that any single workstation can take (i.e., the optimal assembly line duration) is conclusively 70 minutes.

Complexity Analysis of the Optimal Solution using Binary Search:

• Time Complexity: O(N*log(M)), where N represents the number of tasks (or durations) in the list and M represents the sum of all task durations. The key distinction between the brute force approach we previously explored and this solution lies in the method of iteration. Instead of traversing every possible duration between  max(taskDurations)  and   sum(taskDurations)  (which would be  O(M)  in complexity), we employ a binary search strategy. This approach significantly reduces the number of iterations, enhancing efficiency from  O(M)  to  O(log(M)). Hence, the time complexity will improve from  O(N*M)  to  O(N*log(M)).

• Space Complexity: O(1). Our solution does not require additional space; all operations are performed in-place.
  

Below is our coding solution in line with the intuitive walkthrough provided above:

# O(n * log(m)) time | O(1) space
# where 'n' is the length of 'task_durations' and 'm' is the sum of all items in 'task_durations'.
def optimize_tesla_assembly_line(task_durations, num_work_stations):
    # left = min duration possible ; right = max duration possible.
    left, right = max(task_durations), sum(task_durations)
    # max station duration after the assembly line distrib. is optimized.
    max_station_duration = float("inf")

    # Binary search for the best "max" task duration of a work station.
    while left <= right:
        cand_station_duration = (left + right) // 2
        # If the candidate max station duration is possible, then that's the current best we have. 
        if is_possible_station_duration(cand_station_duration, task_durations, num_work_stations):
            max_station_duration = cand_station_duration
            right = cand_station_duration - 1
        else:
            left = cand_station_duration + 1

    return max_station_duration

def is_possible_station_duration(cand_station_duration, task_durations, num_work_stations):
    required_station_num = 1
    curr_duration = 0

    # Check if more than our available work stations is required.
    for task_time in task_durations:
        curr_duration += task_time
        if curr_duration > cand_station_duration:
            curr_duration = task_time
            required_station_num += 1

    # Provided task duration is only possible if we use no more than our limited num of stations.
    return required_station_num <= num_work_stations

Final Notes

If you're preparing for a software engineering role, especially in a company that values innovation and efficiency like Tesla, this problem presents an excellent opportunity to showcase your problem-solving skills. Here are some key takeaways and strategies for this specific challenge:

1. Understanding Efficiency in Production: Grasping the core problem - efficient task distribution across workstations - is critical. At Tesla, where production efficiency is paramount, mastering such optimization problems is invaluable.

2. Operational Constraints: Acknowledge the importance of operational constraints, a common aspect in Tesla's production process. This challenge demonstrates the importance of adhering to specific sequences and operational flows.

3. Innovative Use of Binary Search: Tesla thrives on innovative solutions. Applying binary search in this context shows how thinking outside the box can lead to significant improvements in operational efficiency.

4. Highlighting Complexity Analysis: Discussing the efficiency of binary search over brute force is particularly relevant at Tesla. It showcases your ability to optimize processes, a skill highly valued in Tesla's dynamic environment.

5. Scalability and Real-World Application: Tesla, known for its scalability in production and technology, would appreciate solutions that are not only effective but also scalable. This approach highlights how small time savings can have a substantial impact in large-scale production.

6. Adaptive and Collaborative Problem-Solving: Tesla's fast-paced and innovative culture requires adaptability. Showcasing your ability to think on your feet and collaborate on solutions reflects the ethos of Tesla's work environment.

7. Effective Communication of Complex Ideas: Tesla values clear communication of complex ideas, a critical skill for working in its interdisciplinary teams. Demonstrating this ability through your problem-solving process is crucial.

8. Tesla-Specific Applications: Relate your solution back to Tesla's unique environment. Discuss how this optimization problem, while theoretical, applies directly to scenarios in automobile manufacturing, where Tesla is constantly seeking efficiency enhancements.

In preparing for a role at Tesla, it's essential to show not just your technical skills, but also an understanding of how these skills apply in a practical, innovative, and efficiency-driven environment like Tesla's. Remember, the ability to apply theoretical knowledge to real-world scenarios is highly prized in the tech industry, especially in companies that are at the forefront of innovation.

You got this!