Q2 - Words Search Problem

Consider a rectangular grid where each cell contains a letter. This grid can have different dimensions in terms of its rows and columns, and it represents a game board for word search. Additionally, you have a collection of words.

Your task is to create a function that identifies and returns a list of all words from the given collection that can be formed on the board. The order of the words in the output list is not important.

To form a word, you can connect letters that are adjacent to each other in any direction (up, down, left, right, or diagonally). However, you cannot use the same cell more than once for any single word. Note that the same letter can appear multiple times in different cells and can be used in forming different words. Also, it's possible for different words to share some of the same letters on the board.

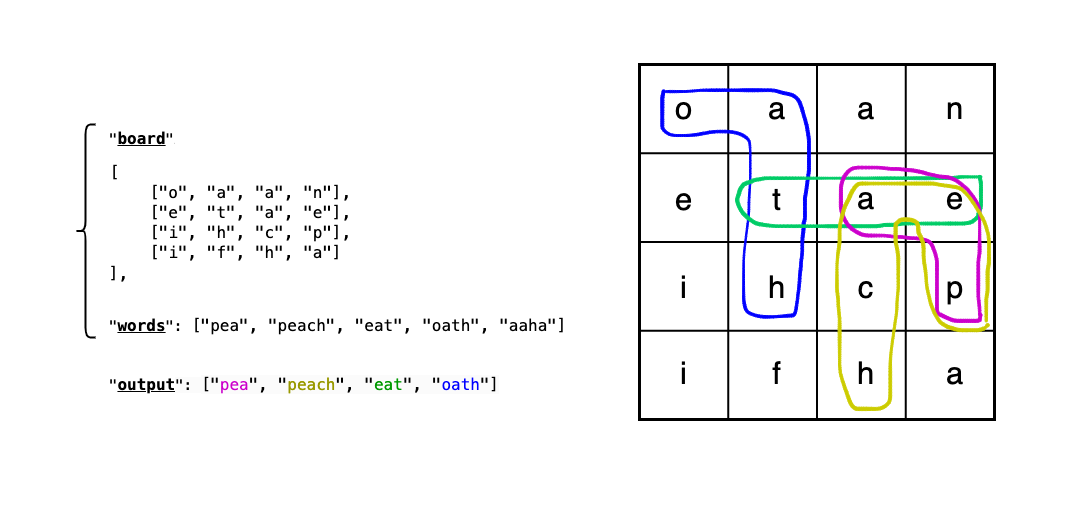
Explanation: "pea", "peach", "eat" and "oath" are the only words that can be formed on the board. We cannot form the word "aaha".

Solution

The brute force approach to solving the word search problem would involve exhaustively checking every possible string that can be formed from the board and then comparing each string against the list of words. This method would require generating all combinations of letters by traversing the board in all directions (horizontally, vertically, and diagonally) from each cell, considering each cell as a starting point. After generating these combinations, each one would be checked against the list of words to see if it matches any of them. This approach, while straightforward, is highly inefficient as it involves a significant amount of redundancy and a large number of comparisons, especially for larger boards and longer word lists.

So, how can we address this problem efficiently? One aspect we cannot avoid is examining each cell on the board as the starting point. We have to do that! This will ensure that we explore all potential word combinations from our input list (or at least attempt to find them). However, we can use an efficient data structure specifically designed for word search and matching problems, namely Trie data structure.

We highly recommend that you have a solid understanding of what a Trie data structure is and how it's used. Please refer to the following resources before continuing: resource-1 and resource-2.

Now that you have a good understanding of what a Trie is, the first step in our solution is to construct a Trie from the input list of words: [pea, peach, eat, oath]. You will see how this will improve the efficiency of our algorithm. We will be using the Example above in our solution.

1) Construct a Trie from the Input List of Words

# Builds a trie from the list of words.
# O(NW) time | O(NW) space where N is the number of words and W is the length of the longest word.
def build_trie(words):
    trie = {}
    for word in words:
        node = trie
        for char in word:
          if char not in node: node[char] = {}
          node = node[char]
        node['END'] = word
    return trie

• Initialize the Trie: We create an empty dictionary named trie. This dictionary will serve as the root of our trie.
• Iterate Through Each Word: We loop through each word in the provided list. For each word, start from the root of the trie (the trie dictionary).
• Building the Trie, Character by Character: For every character in the current word, we check if char is already a key in the current node.
  • If char is not in the current node, we add a new entry in the node with the key as char and the value as an empty dictionary. This step essentially creates a new branch in the trie.
  • We then move to this new node (or the existing node if char was already present).
• Marking the End of a Word: Once all the characters of a word have been added to the trie, the function adds a special key END to the current node. The value of this key is the complete word. This END key signifies that a complete word ends at this node.

Below is the Trie dictionary that is returned by our function:

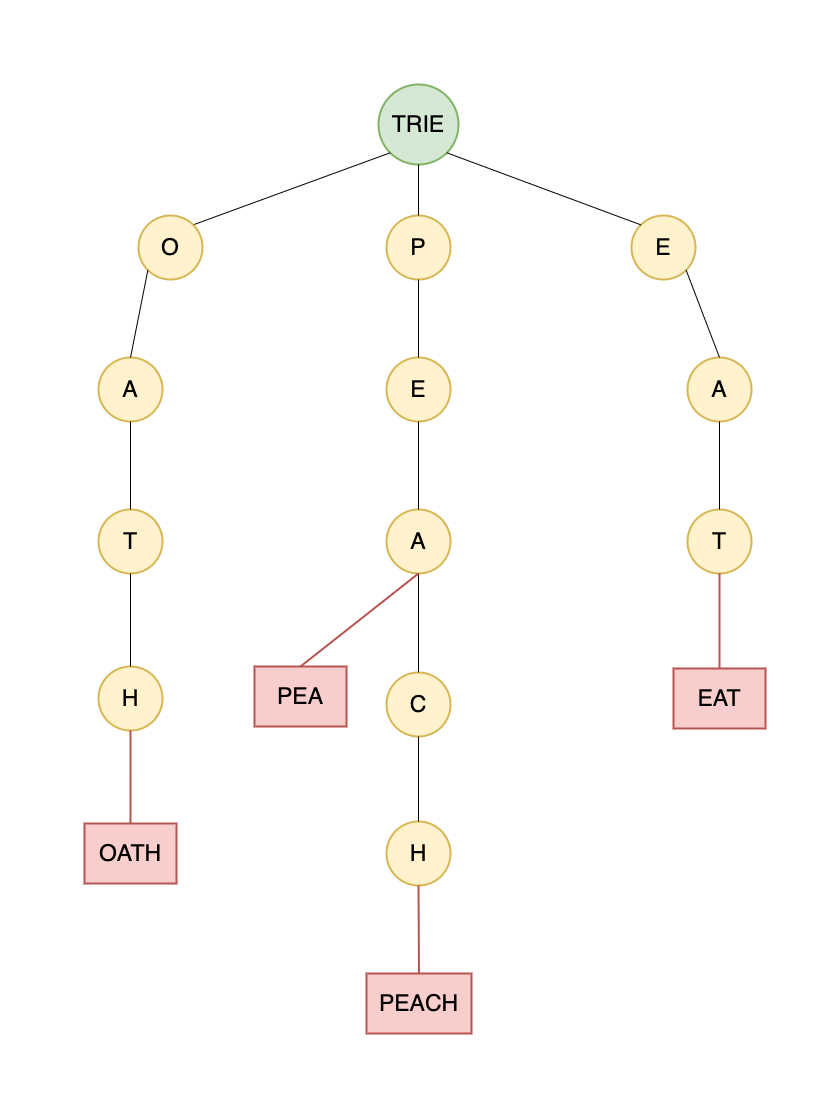
The time and space complexity of this function are O(NW) each, where N is the number of words and W is the length of the longest word. This is because the function potentially needs to create a new node for each character of each word.

2) Iterate Through Each Cell on the Board

    # Iterate through each char in the board
    # ensuring that all possible word combinations are found.
    for r in range(rows):
        for c in range(cols):
            if board[r][c] in trie:
                dfs(r, c, trie[board[r][c]])

Traverse the Board: We go through each cell of the board. Since the board is a grid, we do this by iterating over each row and each column. We cannot avoid examining each cell on the board...

Check for Starting Letters in the Trie: For each cell, we check if the letter in that cell is a starting letter of any word in our trie. This is a crucial step because if the letter isn't a starting letter of any word, there's no point in exploring that path further. As you can see from the Trie that we've constructed in the previous step, the starting letters are: o, p, and e.

Depth-First Search (DFS) for Word Discovery: Whenever we find a letter that is a starting point in our trie, we initiate a depth-first search DFS from that cell. The DFS is a way to explore all possible word paths starting from that letter. It goes deeper and deeper into the board, character by character, to see if we can form a word that exists in our trie.

By doing this for every cell, we make sure that we don't miss any potential words that can be formed on the board. This step is critical in ensuring the thoroughness of our solution.

3) For Each Cell, Perform a DFS to Explore All Possible Paths

# Helper function to perform DFS traversal to find the words.
# O(8^W) time | O(R * C) space where W is the length of the longest word.
def dfs(r, c, node):
    if 'END' in node:
        found_words.add(node['END'])

    visited[r][c] = True # The position is visited, let's discover the neighbours.
    for dr, dc in directions:
        nr, nc = r + dr, c + dc
        if is_valid(nr, nc, rows, cols) and not visited[nr][nc] and board[nr][nc] in node:
            dfs(nr, nc, node[board[nr][nc]])
    visited[r][c] = False # We have exhausted all paths from this char, switch it to False.

Initiating DFS: Whenever we find a letter on the board that is a starting point for a word in our trie, we start a DFS from that cell. The DFS function is called dfs, and it takes the current cell's row and column indices (r and c), and the current node in the trie.

Checking for Word Completion: At each cell visited by the DFS, we check if the current path corresponds to a complete word in the trie (e.g., p -> e -> a -> {"END":"PEA"}). This is indicated by the presence of the END key in the current trie node. If a complete word is found, we add it to our list of found words.

Marking Cells as Visited: To avoid revisiting the same cell in a particular path, we mark the current cell as visited. This is crucial to prevent cycles and redundant searches. Then, we start creating branches from this cell, iterating over its neighbors.

Exploring Neighboring Cells: We explore all its neighboring cells (horizontally, vertically, and diagonally adjacent - a total of 8 directions). For each neighbor, we check if it's valid (within the bounds of the board and not already visited). If the neighbor's letter is the next letter in a potential word (as per our trie), we recursively call our DFS function for that neighbor cell. For instance, consider a scenario where our current branch in the trie is at p -> e -> a -> {"END":"PEA"}, and the adjacent cell on the board contains the letter C. In this situation, we would invoke our DFS function on this neighboring cell and proceed to the next node in the trie. This action is taken because PEACH is one of the words in our list, and this branch might lead to the formation of that word.

Backtracking: After exploring all paths from the current cell, we backtrack by marking the cell as unvisited. This allows the cell to be used in different paths for other potential words.

Below is the visualization of how our DFS function would work where the input cell is the char e:

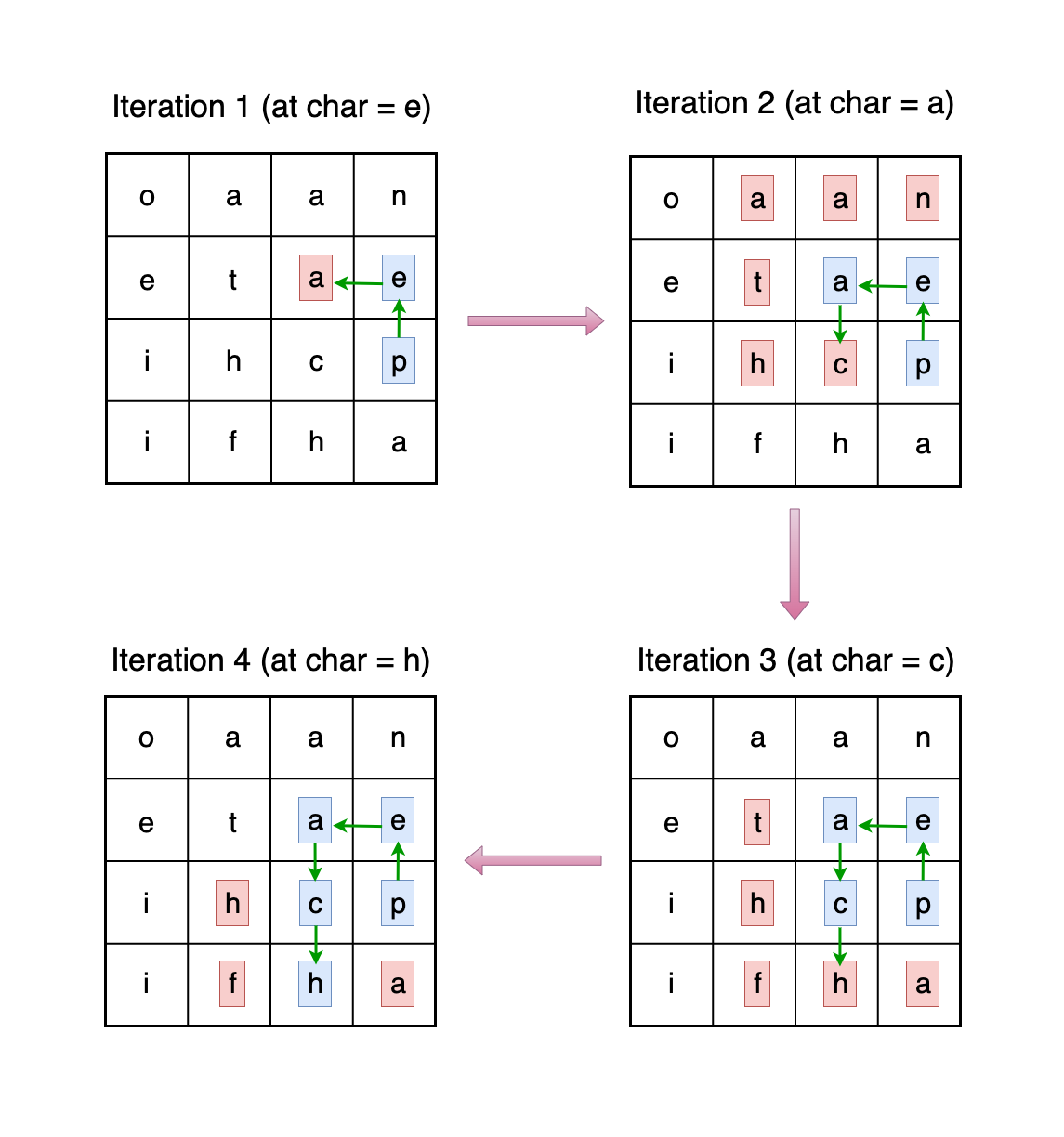
Iteration 1 (At character 'e'): The DFS starts at the character e, examining all adjacent cells for potential next letters. It finds an a next to it, which is the next character in pea and peach. Currently the cell containing a is not visited, hence the red color.

Iteration 2 (At character 'a'): Having moved to a, we find ourselves at a pivotal point. Here, the DFS checks the current trie node for an END key to determine if a valid word has been formed. Since pea is one of our words, and we have reached a following p and e, the trie node would have an {"END":"PEA"} entry, indicating that we have successfully found the word pea. Thus, we add it to our solution list. Moreover, since we will be exploring from this cell a, we mark it as "visited", hence the blue color.

The DFS doesn't stop here, though. It continues to explore further since a could lead to longer words. The neighbors c, a, n, t, h and another a are evaluated (all currently unvisited, hence red). The path following c looks promising for peach, so the DFS proceeds to the cell containing c.

Iteration 3 (At character 'c'): Having moved to c, we mark it as visited, hence the blue color. The path towards peach continues to unfold. The DFS looks around for the next cell containing the letter h (note that there are 2 of these cells. It doesn't matter which one we explore).

Upon finding h in an adjacent cell, we dive deeper with another DFS call to this cell. We can do this because that cell is currently unvisited (red color), so we can explore it.

Iteration 4 (At character 'h'): The arrival at h signifies the potential completion of peach. The DFS checks the trie and indeed finds an {"END":"PEACH"} entry, so we add the word peach to our solution list. As always, we then mark the cell containing h as visited (hence blue).

We would continue exploring further (e.g., unvisited a, f, h chars), even though there is no word extending beyond peach in our list.

Complexity Analysis

Time Complexity: O(R × C × 8^W + NW)

R × C: This represents the traversal of each cell in the grid, where R is the number of rows and C is the number of columns. We initiate the search from every cell.

8^W: For each cell, in the worst-case scenario, we explore all 8 directions (up, down, left, right, and the four diagonals). The depth of this exploration can go up to W, which is the length of the longest word. Therefore, for each cell, the DFS could potentially explore 8^W paths.

R × C × 8^W: Multiplying these factors, we get the total time complexity for the DFS search part, which represents the exhaustive search from every cell in every possible direction to the depth of the longest word.

+N × W: Additionally, we have the time complexity for building the trie. Here, N is the number of words and W is the length of the longest word. Inserting a word into the trie is O(W), and this is done for all N words.

Space Complexity: O(RC + NW)

R × C: We need a 2D array to mark visited cells during DFS. This array has the same dimensions as the board, contributing an R × C factor to the space complexity.

N × W: The trie also occupies space. In the worst case, where each word shares no common prefix with another, the trie's size is proportional to the total number of characters across all words, which is NW.

# O(R * C * 8^W + NW) time | O(R * C + NW) space
def find_words(board, words):
    rows, cols = len(board), len(board[0])
    trie = build_trie(words) # Construct the trie.
    directions = [(0, 1), (0, -1), (1, 0), (-1, 0), (-1, -1), (1, 1), (-1, 1), (1, -1)]
    found_words = set()
    visited = [[False for _ in row] for row in board]

    # Helper function to perform DFS traversal to find the words.
    # O(8^W) time | O(R * C) space where W is the length of the longest word.
    def dfs(r, c, node):
        if 'END' in node:
            found_words.add(node['END'])

        visited[r][c] = True # The position is visited, let's discover the neighbors.
        for dr, dc in directions:
            nr, nc = r + dr, c + dc
            if is_valid(nr, nc, rows, cols) and not visited[nr][nc] and board[nr][nc] in node:
                dfs(nr, nc, node[board[nr][nc]])
        visited[r][c] = False # We have exhausted all paths from this char, switch it to False.

    # Iterate through each char in the board
    # ensuring that all possible word combinations are found.
    for r in range(rows):
        for c in range(cols):
            if board[r][c] in trie:
                dfs(r, c, trie[board[r][c]])

    return list(found_words)

# Builds a trie from the list of words.
# O(NW) time | O(NW) space where N is the number of words and W is the length of the longest word.
def build_trie(words):
    trie = {}
    for word in words:
        node = trie
        for char in word:
          if char not in node: node[char] = {}
          node = node[char]
        node['END'] = word
    return trie

# Checks if the coordinates are within the board.
def is_valid(r, c, rows, cols):
    return 0 <= r < rows and 0 <= c < cols

Final Notes

If you're preparing for a Software Development Engineer interview at Google, there's a fair chance you might encounter the word search question. It's a demanding puzzle, but with strategic preparation, you can ace it. Here are some focused tips for this specific question:

1) Start with the Basic Concept: Initially, discuss the fundamental idea of searching for words in a matrix. This might involve a simple search strategy without optimization. It's essential to lay this groundwork before jumping into more complex solutions.

2) Gradually Introduce the Trie: After covering the basics, steer the conversation towards implementing a trie for efficient word search. This progression from a simple to a sophisticated approach will demonstrate your ability to scale and optimize solutions, a key skill at Google.

3) Emphasize on DFS and Backtracking: Make sure to highlight your understanding of depth-first search (DFS) and backtracking within the matrix. Discussing the reasoning behind choosing DFS over other search techniques will show your analytical skills.

4) Talk Through the Complexity: Be prepared to explain the time and space complexity of your approach in detail. Google interviewers often look for candidates who not only solve the problem but also understand the underlying complexities and can optimize accordingly.

5) Engage in a Collaborative Discussion: If the interviewer suggests alternatives or optimizations, engage with them actively. Show that you are open to feedback and can think on your feet. This is particularly important at Google, where collaborative problem-solving is highly valued.

6) Tailor Your Communication: As you walk through your solution, clearly articulate each step. Google places a high value on candidates who can explain their thought process clearly and concisely.

7) Be Mindful of Prior Knowledge: If you're familiar with this problem, be careful not to reveal the solution too quickly. Instead, work through the problem as if it's a new challenge, using it as an opportunity to showcase your problem-solving and critical thinking abilities in a real-time setting.

Remember, in a Google interview, the journey to the solution is as important as the solution itself. Demonstrating your problem-solving process, ability to optimize, and collaborate effectively are key to making a strong impression.