Q2 - Apple Device Synchronization Sequence Challenge
We believe this interview question has recently been asked by Apple to full-time software engineering candidates at all levels.
In the seamless ecosystem of Apple, synchronizing content across devices is a regular task that requires precision and flexibility. As a software engineer at Apple, you are tasked with developing a synchronization sequence for user settings that are distributed across different devices—like an iPhone, iPad, or MacBook. Each setting is represented by a character, and a user's preferred settings are stored as a sequence of characters.
Imagine you have a large string that represents the cumulative settings from a user's devices in no particular order. You are also given a smaller string that represents the essential settings that must be synchronized to initiate a user's session. Your function must determine the shortest sequence of settings within the larger string that contains all the necessary settings from the smaller string, regardless of order.
Considerations for the Synchronization Algorithm:
- The shortest sequence can include additional settings not found in the essential settings list.
- The settings in the sequence do not have to synchronize in the same order as they appear in the user's preferences.
- If a particular setting is required more than once, the sequence must include it as many times as needed.
This synchronization sequence algorithm will ensure that users have all their essential settings in place as quickly as possible, enhancing their experience with Apple's interconnected devices.
Below are two examples:
Example 1
Input:
largeString: "thisisateststring"
targetString: "tist"
Output: "tstri"
Example 2
Input:
largeString: "k65tzj6qjy5jr"
targetString: "j56jq"
Output: "j6qjy5"
Solution 1
This challenging problem has frequently appeared in Apple's interviews, so it is crucial that you understand how to tackle it! The problem involves searching through a large string to find the smallest possible substring that contains all the characters of a given target string, accounting for the frequency of each character as they appear in the target string. This problem is a variant of the "minimum window substring" problem which is common in interviews for roles involving algorithms, such as those at major tech companies.
Below we will provide a high-level overview of the solution before jumping into each section:
- Character Frequency Mapping: First, we construct a dictionary to count the frequency of each character in the target string. This helps us understand exactly what we need to look for in the larger string.
- Sliding Window Technique: Utilizing two pointers (
left_idxandright_idx), we create a dynamic window in the large string. This window expands and contracts to encompass a substring that potentially contains all the characters from the target string with their respective counts. - Expanding the Window: Starting with both pointers at the beginning of the large string, we move
right_idxto the right, expanding our window until it includes all the required characters of the target string. - Contracting the Window: During the process of contracting, we continually update the boundaries of our smallest valid substring.
- Updating the Smallest Substring: Throughout the process, we track and update the boundaries of the smallest valid substring whenever we find a better candidate.
To gain a clearer visualization of how the algorithm functions, please refer to the Visual Demonstration of Example-2 section at the bottom of this page.
1) Character Frequency Mapping
The first step in the solution is to create a frequency dictionary (target_char_counts) for the target string, which records the number of times each character needs to appear in the substring
we are looking for. This dictionary will guide the entire search process by defining what we need to find in the large string. Below is the code snippet to generate this dictionary:
# Main function.
# O(n + m) time | O(n + m) space
def find_smallest_substr_containing_target(large_string, target_string):
# Our target char count dictionary:
# target_string = "aabcc&" => {'a': 2, 'b': 1, 'c': 2, '&': 1}
target_char_counts = Counter(target_string)
...
The Counter class is a built-in utility in Python. To understand how to populate the frequency dictionary in other languages,
check out the coding solution section below.
Let's consider the second example (e.g., Example-2):
Example
Input:
largeString: "k65tzj6qjy5jr"
targetString: "j56jq"
The constructed target_char_counts dictionary would be:
Constructed 'target_char_counts' dictionary
target_char_counts = {'j': 2, '5': 1, '6': 1, 'q': 1}
This implies that our output string must include at least two occurrences of 'j', one occurrence of '5', one occurrence of '6', and one occurrence of 'q'.
2) Sliding Window Technique
This step involves two pointers, left_idx and right_idx, which define a sliding window on the large string. The goal is to expand this window to include all the necessary characters and
then contract it to find the smallest possible substring containing all characters of the target string.
- Starting Point: Both pointers are at the beginning of the large string:
left_idx = 0 ; right_idx = 0 - Expanding: Move
right_idxto include more characters. - Contracting: Once all target characters are included, move
left_idxto make the window smaller but still valid.
Below are some of the variables that we will need before starting the sliding window process:
# Main function.
def find_smallest_substr_containing_target(large_string, target_string):
# Our target char count dictionary:
# target_string = "aabcc&" => {'a': 2, 'b': 1, 'c': 2, '&': 1}
target_char_counts = Counter(target_string)
# How many unique chars in the target string have we fully found so far?
unique_target_chars_hit = 0
# The left and right indices of the smallest substring containing all the
# chars in 'target_string'.
smallest_substr_interval = [float("-inf"), float("inf")]
# Current substring's char counts.
substr_char_counts = defaultdict(lambda: 0)
left_idx, right_idx = 0, 0
- unique_target_chars_hit: This variable tracks how many of the required unique characters from the target string are currently fully matched in the sliding window on the larger string.
Initially set to zero, it increments each time a character's count in the current window matches the count needed as specified in
target_char_counts. For instance, ourtarget_string = j56jqcontains two occurrences of j. This means that we need to discover two j's to increment ourunique_target_chars_hitby one. - smallest_substr_interval: This variable keeps track of the start and end indices of the smallest substring found so far that contains all the target characters with their required frequencies.
It starts with the default values
[float("-inf"), float("inf")], indicating an infinitely large range that will be updated as smaller valid substrings are identified.
We store the indices of the smallest substring instead of slicing the string directly. This approach is efficient because, in some programming languages, slicing a string to create a new substring would take O(n) time. By storing indices, we bypass this additional time complexity, which is a common practice. Keep in mind that talking about this decision for optimized performance to your interviewer would demonstrate your attention to detail and efficiency!
- substr_char_counts: This dictionary maintains the count of each character as it appears in the current window of the
large_string. It is vital for dynamically checking whether the current window has the characters in the necessary frequencies as specified in thetarget_char_counts. - Left and Right Indices (left_idx, right_idx): These indices represent the current window in the
large_stringthat is being examined. Theright_idxis incrementally moved to the right to expand the window, and for each position, the character atright_idxis evaluated:- If it is part of the target, its count is updated in
substr_char_counts. - If its updated count matches the required count from
target_char_counts,unique_target_chars_hitis incremented.
- If it is part of the target, its count is updated in
As soon as unique_target_chars_hit matches len(target_char_counts) (e.g., number of unique chars in the target_string), it means the current window contains all required characters in the necessary counts, and then left_idx starts moving
right to contract the window from the left to determine the smallest possible valid substring. During this contraction, if a character's count falls below what is needed, unique_target_chars_hit
is decremented, and the window needs to be expanded again from the right.
We will go through this process using our Example-2.
3) Expanding the Window
The process of expanding the window is central to the sliding window technique used in our solution for finding the smallest substring that contains all the characters of the target string with the required frequencies. Here's a detailed explanation of how we handle the expansion of the window:
a) Moving the Right Index and Updating Character Counts (right_idx)
# Current substring's char counts.
substr_char_counts = defaultdict(lambda: 0)
left_idx, right_idx = 0, 0
# 'right_idx' will be shifted to the right until it includes all the required
# characters from the 'target_string', accounting for their frequency as they
# appear in the target_string.
while right_idx < len(large_string):
right_char = large_string[right_idx]
...
The expansion phase starts with the right index (right_idx) at the beginning of the large_string. This index is incremented step-by-step, moving through the large_string from left to right.
For each increment:
- We capture the character at the current
right_idxposition in thelarge_string. - This character is referred to as
right_char.
Observe in the image below that we initialize left_idx = right_idx = 0:
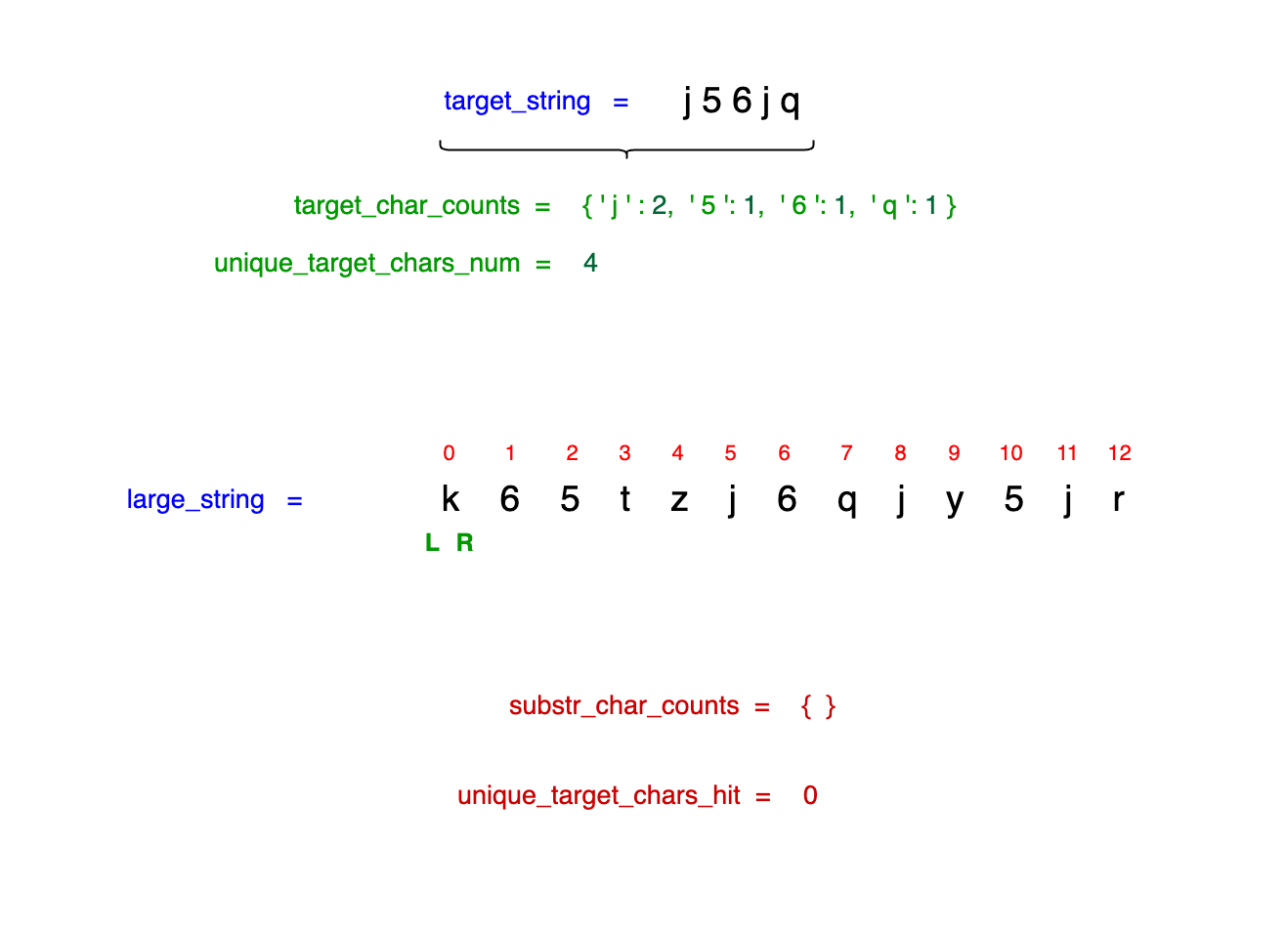
Since we have not yet found all our target characters, we need to expand our window by incrementing right_idx. Each time we encounter a target character, we track it in our
substr_char_counts. We only increment unique_target_chars_hit when a target character is encountered sufficiently to match its required frequency in the target_string :
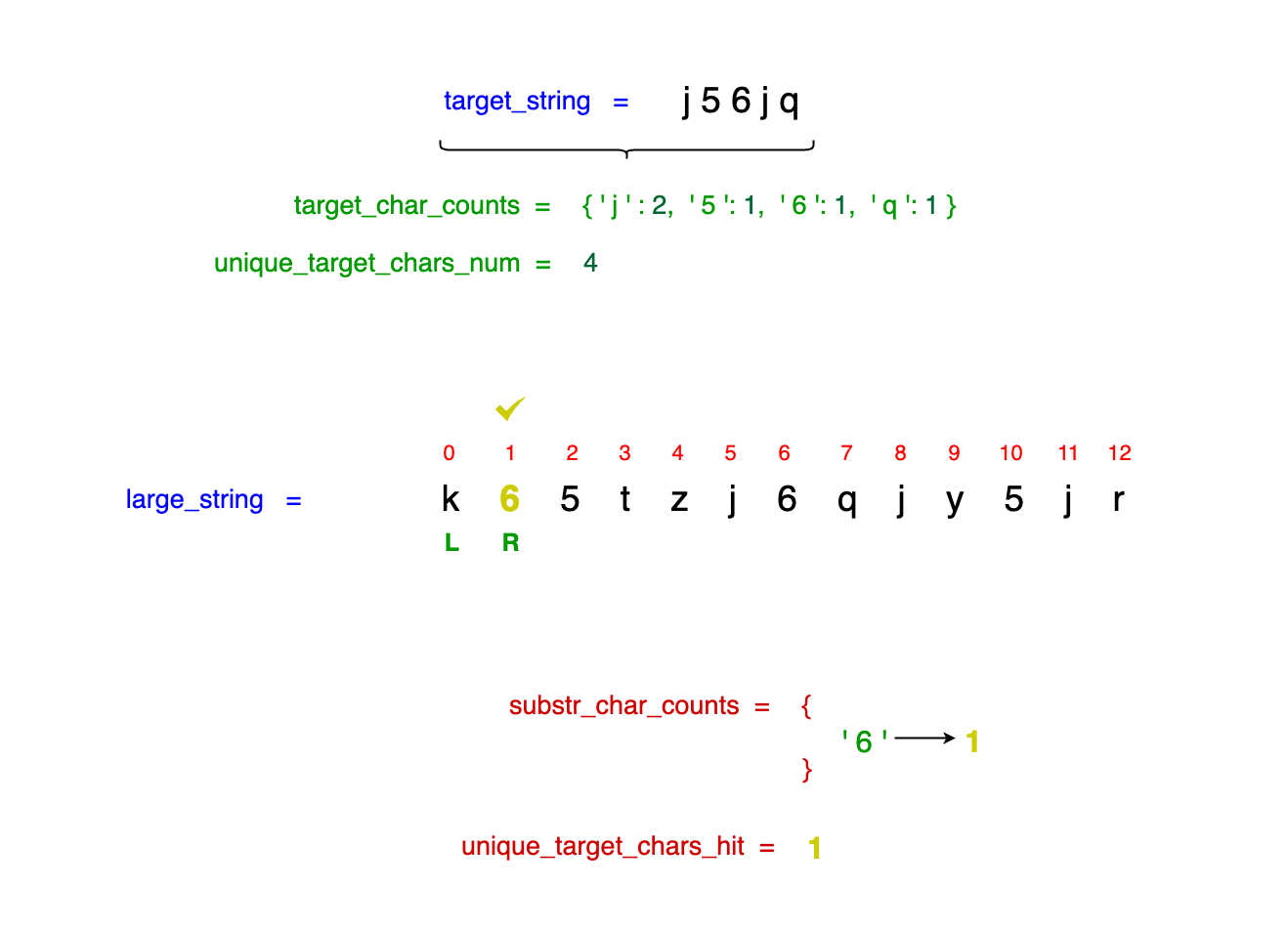
Notice that the first character we encounter is '6'. We track its occurrence in our substr_char_counts dictionary, which now reads {'6' --> 1}. Given that the character '6'
appears only once in our target_string (j56jq), we increment unique_target_chars_hit to 1.
Furthermore, as we have not yet encountered all the required characters from j56jq, we cannot begin to contract our window. Instead, we must continue to expand it by incrementing right_idx.
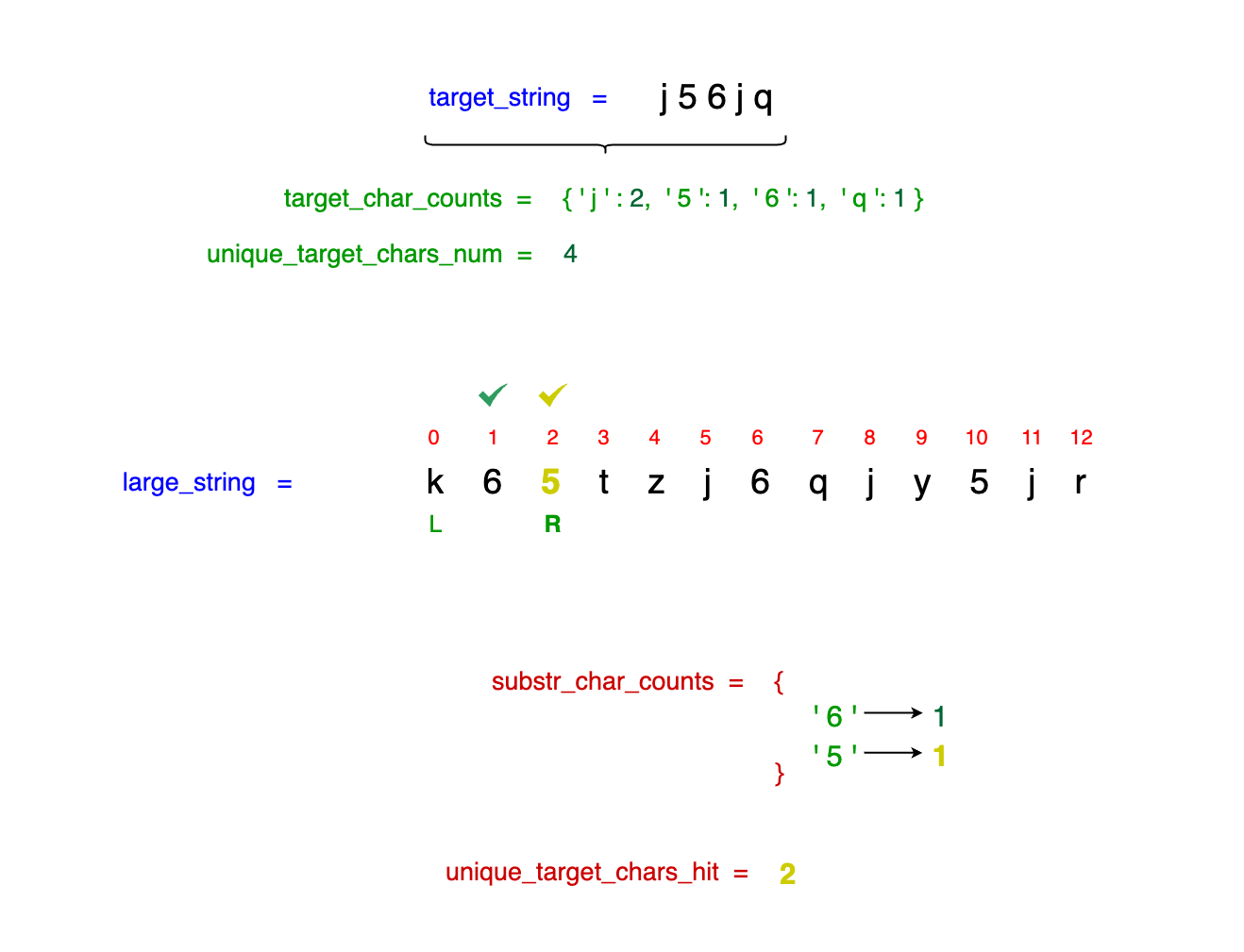
As we continue to increment our right_idx, we encounter the character '5', which is also in our target_string (j56jq). We update our dictionary to reflect this occurrence: {'5' --> 1}.
Since '5' appears only once in the target_string, we increase unique_target_chars_hit to 1 + 1 = 2. At this point, we have successfully found two of the required characters: 5 and 6.
The formal process is as follows:
Once right_char is identified, several actions occur based on its relevance to the target_string:
- Check Relevance: Determine if
right_charis part of thetarget_char_counts dictionary(i.e., it is a character that the target string requires). - Update Counts: If
right_charis relevant, update thesubstr_char_countsdictionary to increment the count ofright_char:- Check if
right_charis already in thesubstr_char_countsdictionary. - If it is not, initialize its count to
0. - Increment the count of
right_charby1.
- Check if
Below is a code snippet illustrating the process described above:
# Current substring's char counts.
substr_char_counts = defaultdict(lambda: 0)
left_idx, right_idx = 0, 0
# 'right_idx' will be shifted to the right until it includes all the required
# characters from the 'target_string', accounting for their frequency as they
# appear in the target_string.
while right_idx < len(large_string):
right_char = large_string[right_idx]
# If the encountered char is not a target char, we simply continue.
if right_char not in target_char_counts:
right_idx += 1
continue
# We have encountered a target char. Increment its count in our dictionary.
substr_char_counts[right_char] += 1
...
b) Matching Target Requirements
After updating the count of right_char:
- Check Full Match: Compare the updated count of
right_charinsubstr_char_countswith its required count intarget_char_counts. - Record Achievement: If the count matches the requirement (meaning we have found enough instances of
right_charas required by thetarget_string), increase theunique_target_chars_hitby1. This indicates that one more unique character from thetarget_stringhas been fully matched in the current window.
# We have encountered a target char. Increment its count in our dictionary.
substr_char_counts[right_char] += 1
# If we encountered the target char enough times, mark it as fulfilled!
if substr_char_counts[right_char] == target_char_counts[right_char]:
unique_target_chars_hit += 1
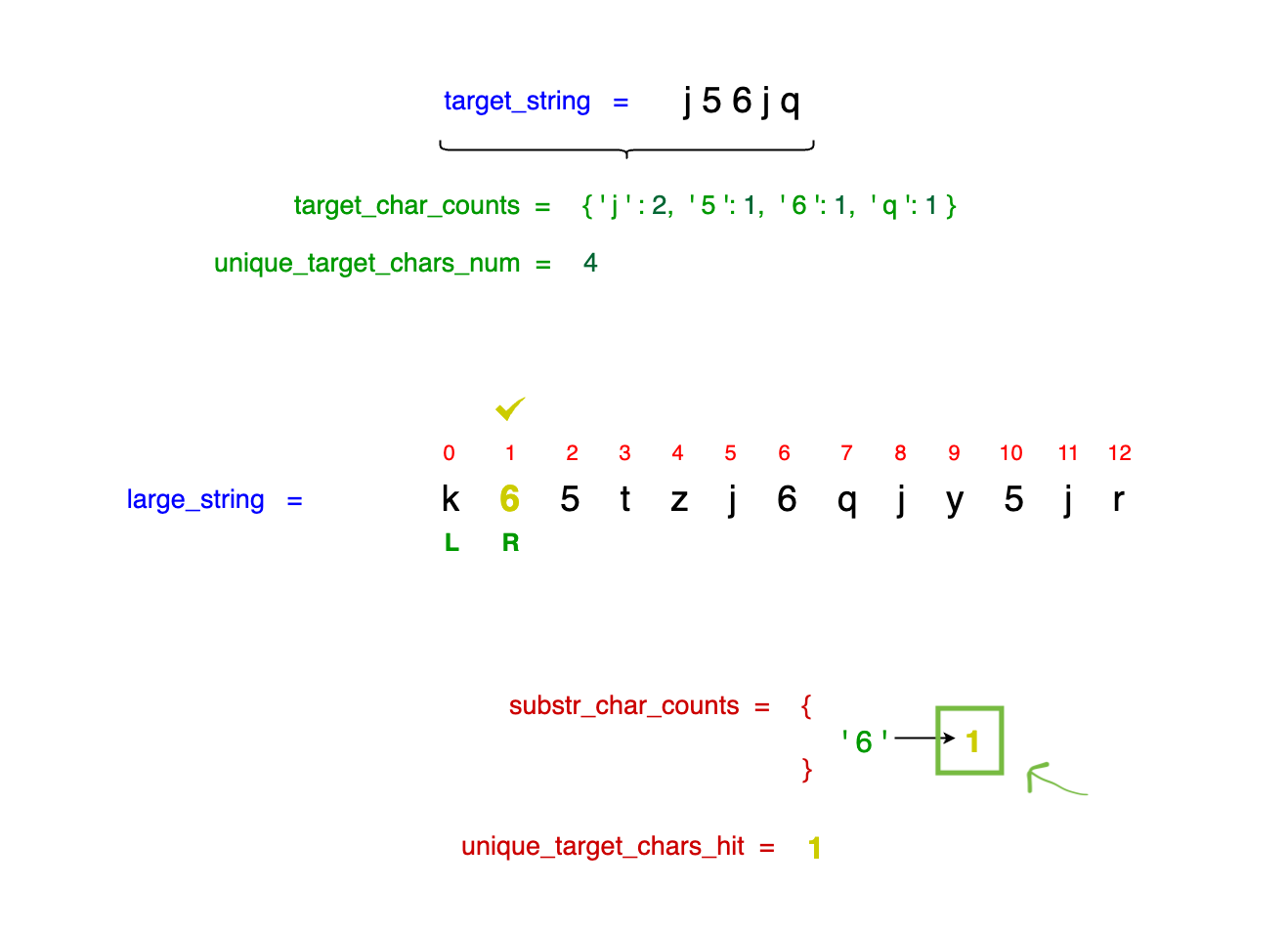
As mentioned previously, given that the character '6' appears only once in our target_string (j56jq), we increment unique_target_chars_hit to 1:
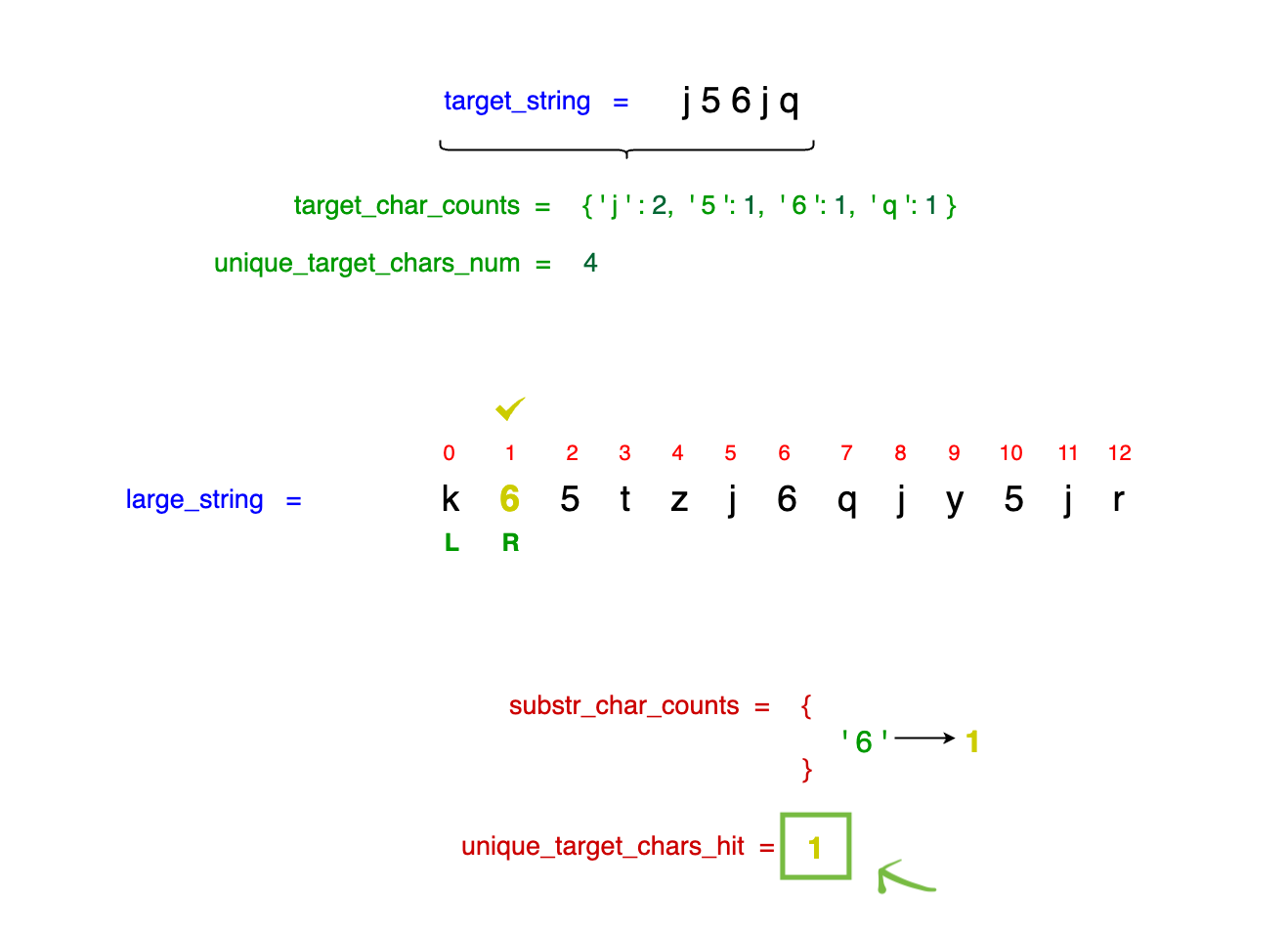
Observe in the image below that although we encounter our first j, we do not increment unique_target_chars_hit. This is because the target_string (j56jq) requires two occurrences of j
for it to be considered fully hit.
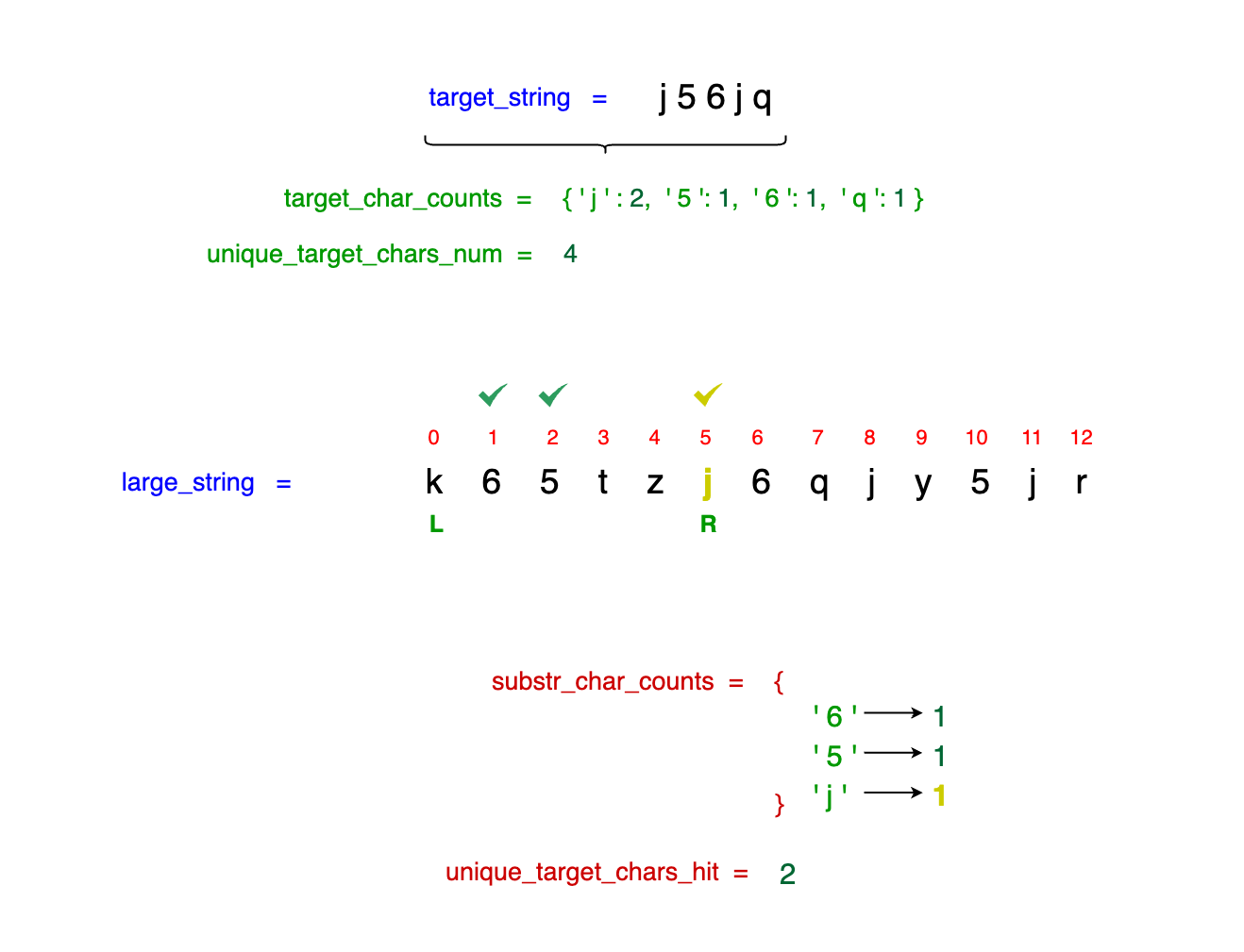
c) Evaluating Window Validity
With each move of right_idx and potential increment of unique_target_chars_hit:
- Check Window Validity: Evaluate whether the
unique_target_chars_hitequalsunique_target_chars_num = len(target_char_counts)(which means the current window has all the required characters of thetarget_stringwith at least the required frequencies). - Update Smallest Bounds: If the current window is valid, potentially update the smallest substring bounds by comparing the current window
size with the smallest found so far. This comparison is managed by another helper function
find_smallest_interval.
Below is a code snippet illustrating the process described above:
# We have encountered a target char. Increment its count in our dictionary.
substr_char_counts[right_char] += 1
# If we encountered the target char enough times, mark it as fulfilled!
if substr_char_counts[right_char] == target_char_counts[right_char]:
unique_target_chars_hit += 1
# We move the 'left_idx' to the right until the substring between 'left_idx' and
# 'right_idx' no longer contains a sufficient number of the required target chars.
# The purpose of this is to find the smallest substring that contains all the target
# chars (each at least as frequent as they appear in the 'target_string').
# e.g., target_string = "aabcc&" => len(target_char_counts) = 4.
while left_idx <= right_idx and unique_target_chars_hit == len(target_char_counts):
# Is the candidate substring the smallest one we ever found?
smallest_substr_interval = find_smallest_interval(smallest_substr_interval, left_idx, right_idx)
...
# O(1) time | O(1) space.
# Helper method to compare a candidate substring with the current smallest substring.
def find_smallest_interval(curr_substr_interval, left_idx, right_idx):
if curr_substr_interval[1] - curr_substr_interval[0] < right_idx - left_idx:
return curr_substr_interval
return [left_idx, right_idx]
When the right_idx reaches idx = 8, marking the second occurrence of j, our current window for the first time contains all the required characters of the target_string,
meeting or exceeding their required frequencies. This condition is reflected in our substr_char_counts as illustrated in the diagram below. Consequently, we can identify a substring
that encapsulates all required characters from the target_string. Since this is the first occurrence of such a complete substring, it is currently the smallest_substr_found:
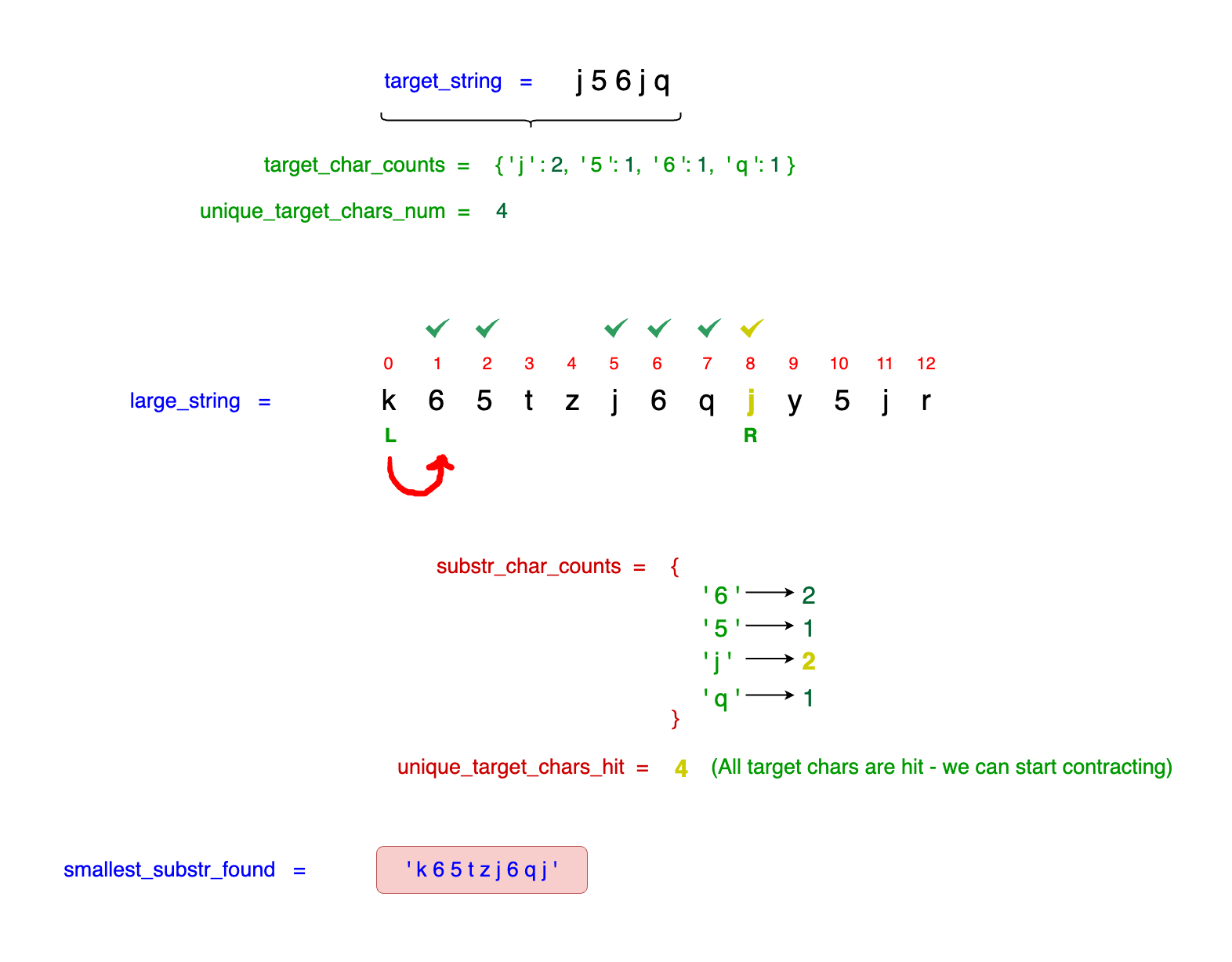
Observe that we've identified our first potential substring - k65tzj6qj - which encapsulates all the required characters from the target_string, each meeting or
exceeding their necessary frequencies. At this point, we can begin the process of contracting our window. This is to ascertain whether a more concise substring exists that
fulfills the character requirements from the target_string without sacrificing the frequency stipulations.
4) Contracting the Window
Once we have expanded our window such that it includes all the required characters from the target_string with the necessary frequencies, the next logical step is to attempt to
minimize or contract this window. This phase is crucial as it directly impacts the efficiency and optimality of the solution—our goal is to find the smallest possible substring that
fulfills the character requirements.
- At this stage,
right_idxhas just included a character that allows the window to satisfy all character requirements fromtarget_string. unique_target_chars_hitequalsunique_target_chars_num, indicating that all distinct characters fromtarget_stringhave been accounted for in the current window with the required frequencies.
Below is the code snippet showing the necessary conditions to start the process of contracting:
# We move the 'left_idx' to the right until the substring between 'left_idx' and
# 'right_idx' no longer contains a sufficient number of the required target chars.
# The purpose of this is to find the smallest substring that contains all the target
# chars (each at least as frequent as they appear in the 'target_string').
# e.g., target_string = "aabcc&" => len(target_char_counts) = 4.
while left_idx <= right_idx and unique_target_chars_hit == len(target_char_counts):
# Is the candidate substring the smallest one we ever found?
smallest_substr_interval = find_smallest_interval(smallest_substr_interval, left_idx, right_idx)
...
You can also observe that we have all the necessary conditions at this point:

- We start moving the
left_idxrightward to reduce the size of the current window. Each step involves analyzing whether the window still contains all the necessary characters fromtarget_string. - This contraction continues until the condition of containing all target characters is just about to break, which is when one of the character's frequency in the window falls below the required frequency in target_string.
Notice that our left_idx is at 0, corresponding to the character k. Given that k is not part of our target_string, we can safely advance our left_idx to the next position. This is
shown in the diagram below.

Here is the code snippet demonstrating how we can safely continue the process of contracting the window by moving our left_idx forward. Since the character k is not part of
the target_string, it does not affect the inclusion of all target characters within the window. We can move left_idx from idx = 0 to idx = 1:
while left_idx <= right_idx and unique_target_chars_hit == len(target_char_counts):
# Is the candidate substring the smallest one we ever found?
smallest_substr_interval = find_smallest_interval(smallest_substr_interval, left_idx, right_idx)
left_char = large_string[left_idx]
# The encountered char is a target char. Thus, we need to decrease its frequency.
if left_char in target_char_counts:
# Omitted logic...
left_idx += 1 # If the left_char is not a target char, just move forward.
...
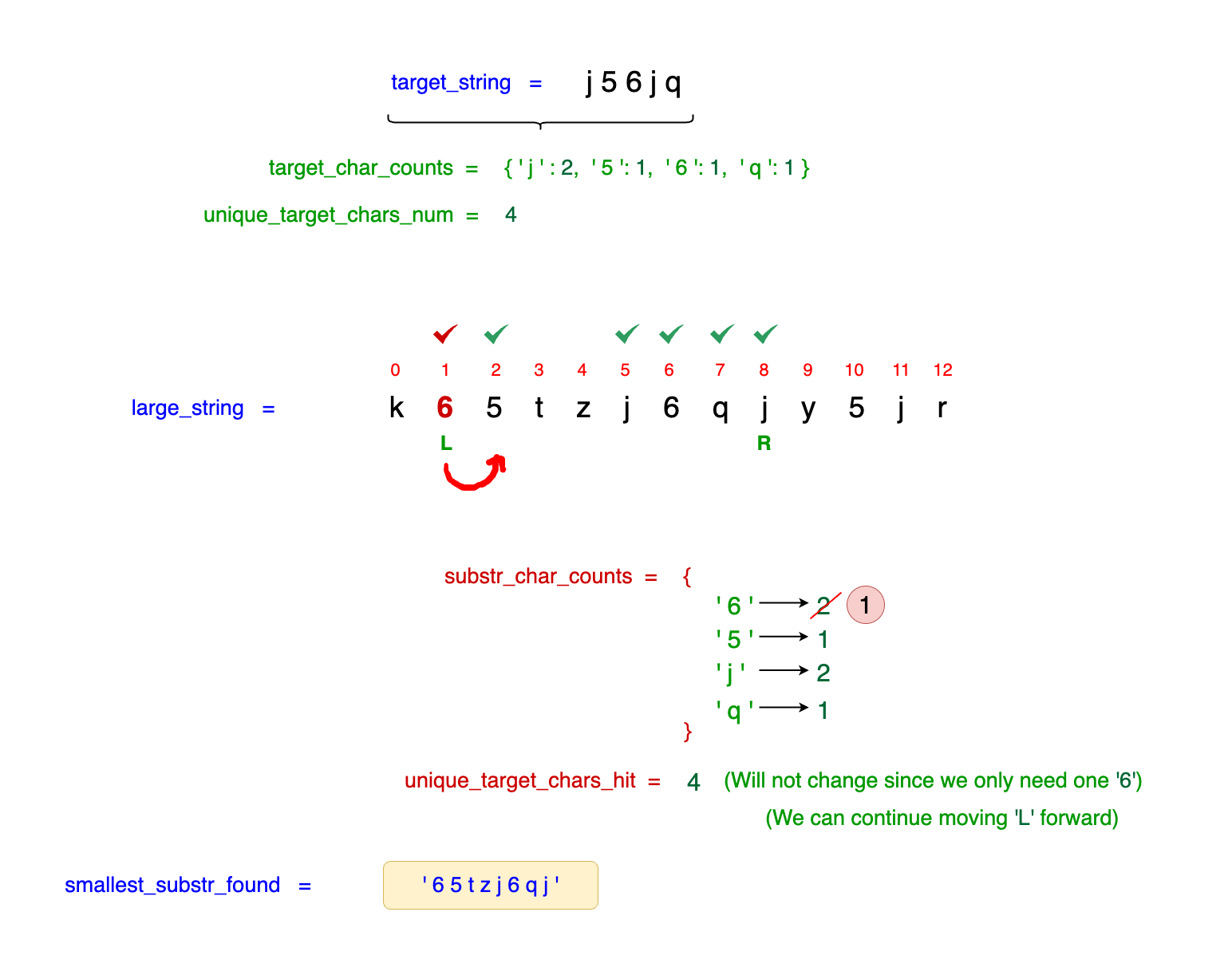
The current substring ( e.g., large_string[L : R]) is the new smallest substring - 65tzj6qj.
c) Adjustments and Checks
Again, for every character at left_idx:
- If it is not a target character, simply increment
left_idxbecause its presence or absence does not impact the requirement fulfillment. This was shown in the code snippet above. - If it is a target character, decrement its count in
substr_char_counts. - After decrementing, check if this character's count is now less than what is required as per
target_string. If so, decrementunique_target_chars_hitby one because we now have one less character meeting its required frequency. - This decrement signifies that the current window can no longer be considered valid in terms of containing all necessary characters, hence stopping the contraction process.
Observe that our left_idx is currently at idx = 1, which corresponds to the character 6. Although 6 is a part of our target_string, we can still advance our left_idx to idx = 2
without excluding any necessary characters. This move is feasible because our current window contains two instances of 6, while the target_string requires only one. Consequently,
we can safely increment our left_idx, but we must adjust by decrementing its count in substr_char_count to maintain accurate tracking:

Here is the code snippet showing the process of decrementing target char's count in substr_char_count:
while left_idx <= right_idx and unique_target_chars_hit == len(target_char_counts):
# Is the candidate substring the smallest one we ever found?
smallest_substr_interval = find_smallest_interval(smallest_substr_interval, left_idx, right_idx)
left_char = large_string[left_idx]
# The encountered char is a target char. Thus, we need to decrease its frequency.
if left_char in target_char_counts:
substr_char_counts[left_char] -= 1
...
This move results in the diagram below. Notice that our left_idx is now at idx = 2, which corresponds to char = 5. Our current substring is now the smallest substring that
contains all the necessary target chars enough times: 5tzj6qj.
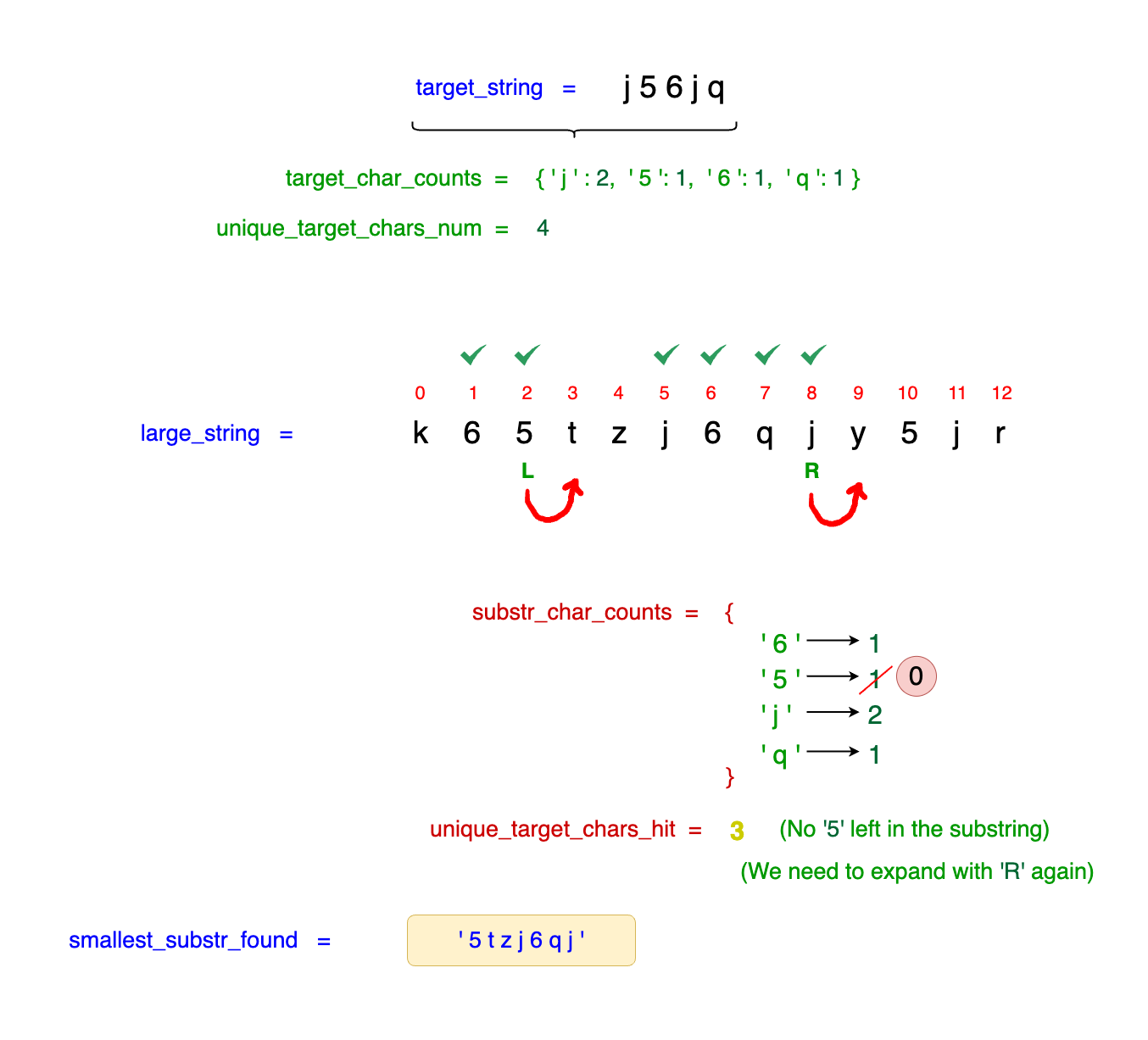
However, at idx = 2, we encounter the character 5. As we move our left_idx from idx = 2 to idx = 3, we lose our only instance of 5. Although this adjustment is
part of the contracting process to potentially find a smaller valid substring, it results in a substring that no longer meets all requirements of the target_string. This necessitates expanding
the window again by shifting the right_idx forward to recover the lost 5 or find another valid configuration.
Observe in the diagram above that the count of char = 5 decreases to 0, indicating that our substring no longer contains any 5s. Consequently, our unique_target_chars_hit
decreases from 4 to 3. This change signals that further contraction of the window is not viable while still meeting all conditions, necessitating a shift back to expanding the window by
moving the right_idx forward.
Here is the code snippet that illustrates the transition from contracting to expanding the window when we encounter a situation where a necessary character's count drops below the required threshold:
while left_idx <= right_idx and unique_target_chars_hit == len(target_char_counts):
# Is the candidate substring the smallest one we ever found?
smallest_substr_interval = find_smallest_interval(smallest_substr_interval, left_idx, right_idx)
left_char = large_string[left_idx]
# The encountered char is a target char. Thus, we need to decrease its frequency.
if left_char in target_char_counts:
substr_char_counts[left_char] -= 1
# The char count may go below its frequency in the 'targetString'.
# In which case, we would need to decrement the 'unique_target_chars_hit'.
if substr_char_counts[left_char] < target_char_counts[left_char]:
unique_target_chars_hit -= 1
left_idx += 1
...
Observe in the code below how the decrease in unique_target_chars_hit signifies the end of the contraction phase. This adjustment occurs because the substring no longer maintains
all the necessary characters from the target_string with the required frequencies. In this example, the missing required char is 5.
# The encountered char is a target char. Thus, we need to decrease its frequency.
if left_char in target_char_counts:
substr_char_counts[left_char] -= 1
# The char count may go below its frequency in the 'targetString'.
# In which case, we would need to decrement the 'unique_target_chars_hit'.
if substr_char_counts[left_char] < target_char_counts[left_char]:
unique_target_chars_hit -= 1
left_idx += 1
So, what do we do now? We go back to the previous step: Expanding the Window.
We proceed to expand the window by incrementing the right_idx. This expansion continues until the substring once again contains all the required characters from the target_string,
each with the correct frequencies. The expansion stops at idx = 10:
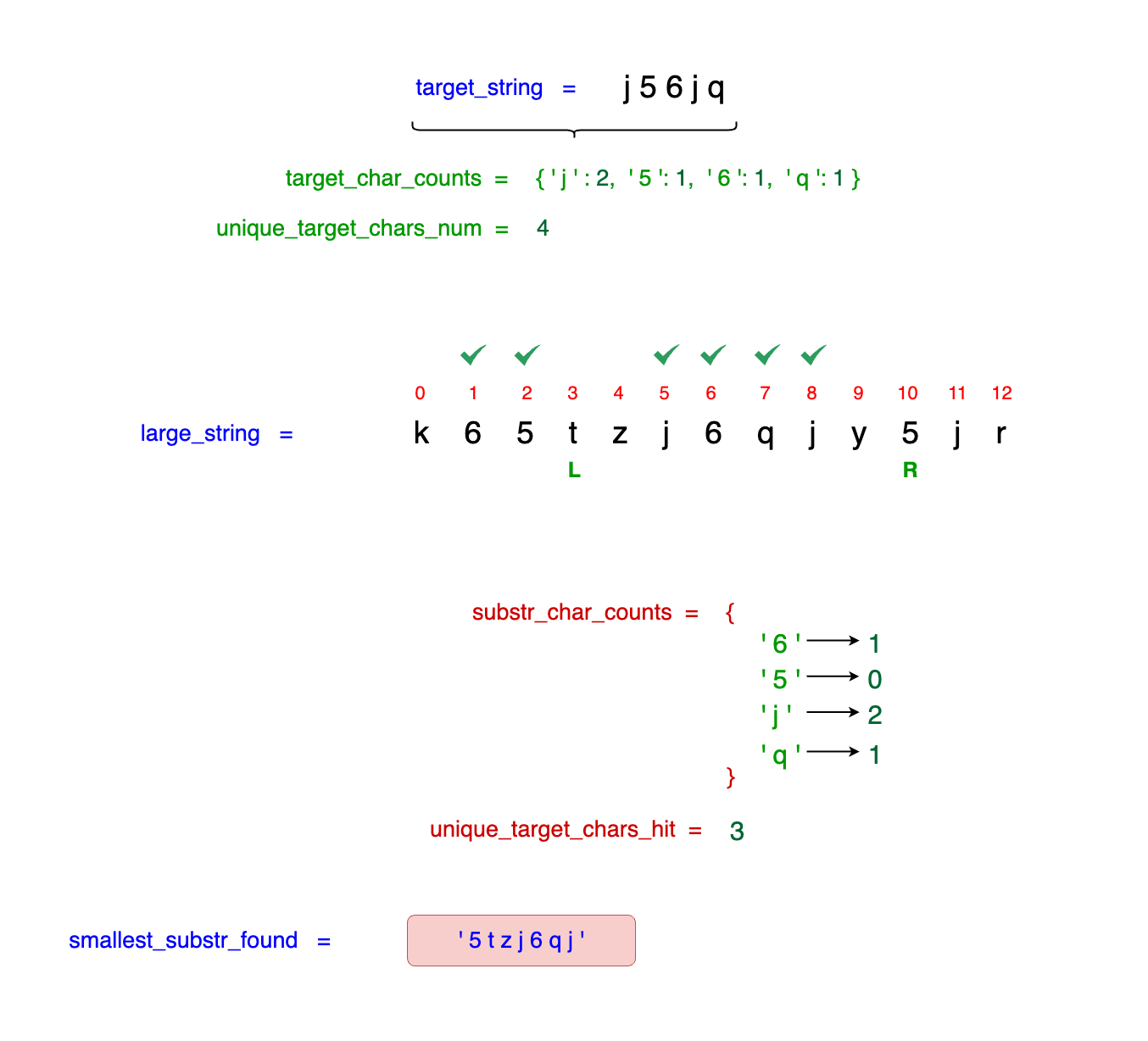
We move the right_idx up until idx = 10, which has our missing char - 5. The corresponding substring - tzj6qjy5 - contains all the required characters. Hence, we can start the
process of contracting once again:
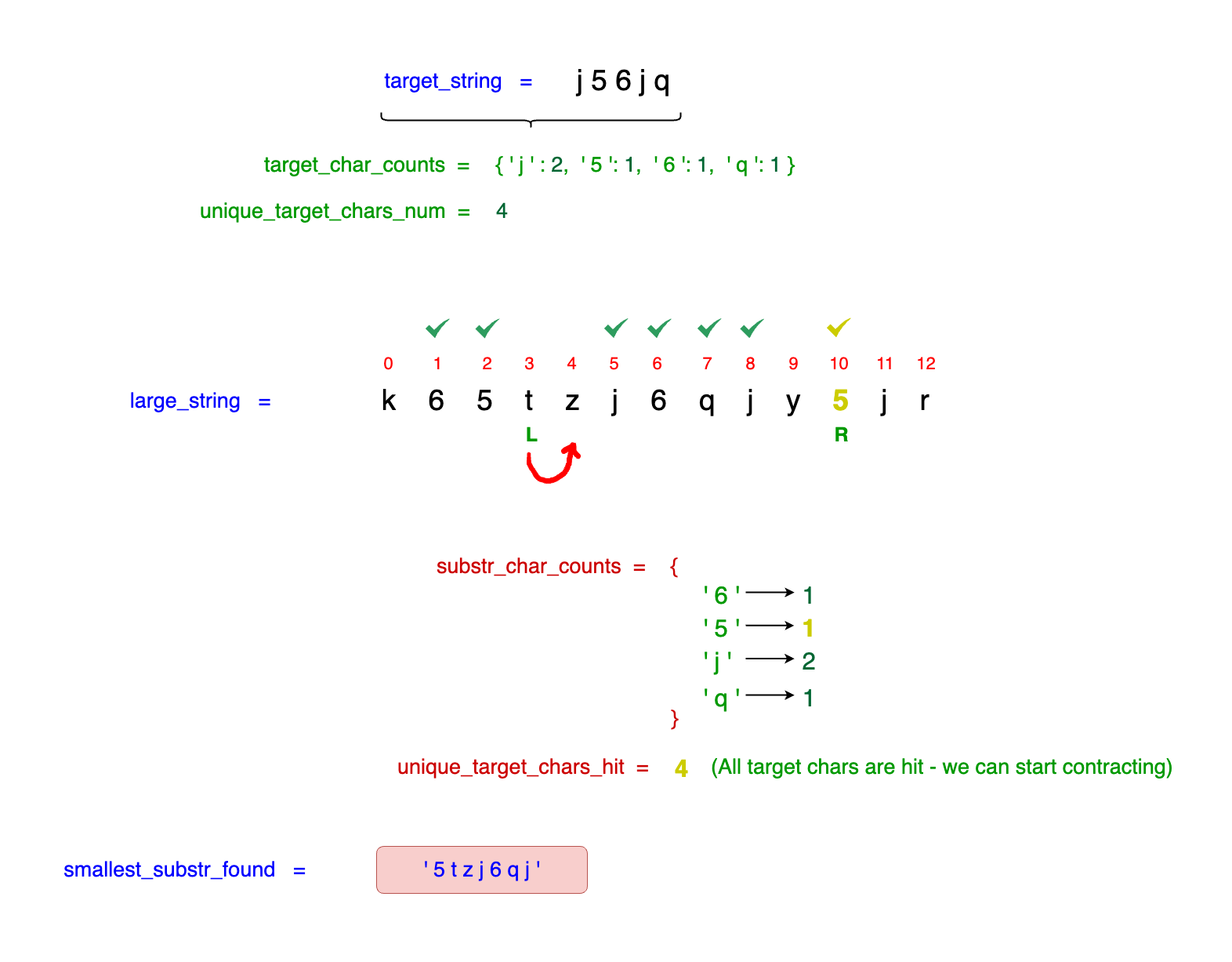
The contraction goes until we reach left_idx = 5. Moreover, the resulting substring is the smallest substring containing all the required characters - j6qjy5 with a length equal to 6.
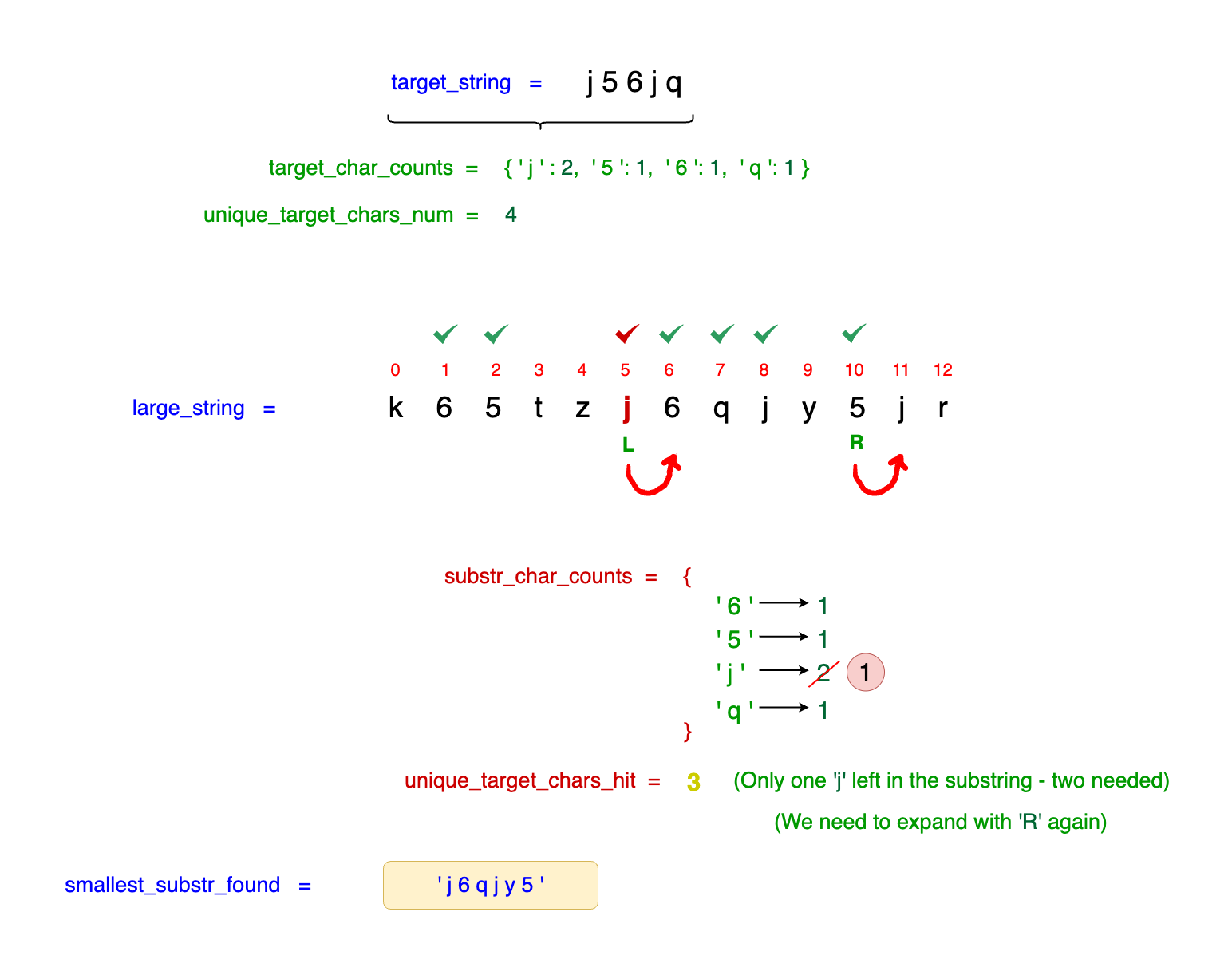
When we advance the left_idx to idx = 6, we lose one instance of j, reducing the count to just one remaining j in our substring. This reduction causes the unique_target_chars_hit
to drop below the required 4. As a result, the contraction process stops, and we must resume expanding by moving the right_idx forward.
Below, we provide a step-by-step visual demonstration of Example-2. Each image corresponds to a specific step in the sequence, illustrating the progression of the algorithm's operation.
Visual Demonstration of Example-2

Complexity Analysis
-
Time Complexity: O(N + M), where N represents the length of the
large_string, and M represents the length of thetarget_string. The time complexity of the algorithm is determined by a few key operations that occur as we iterate through thelarge_stringand manage thetarget_stringcharacters.Explanation:
-
Constructing Character Counts
- Initially, we construct a dictionary (
target_char_counts) from thetarget_string, where we count the occurrences of each character. This operation is O(M) time, where M is the length oftarget_string.
- Initially, we construct a dictionary (
-
Sliding Window Mechanism
- Expanding the Window: We iterate through each character in the
large_stringwith theright_idx. As we do so, we potentially update oursubstr_char_countsdictionary if the character is intarget_char_counts. This step involves checking and inserting characters into a dictionary, which on average takes O(1) time for each character due to the average-case time complexity of hash table operations. Thus, iterating through the large_string takes O(N), where N is the length oflarge_string. - Contracting the Window: Once a valid window is found (one that contains all characters from
target_string), we attempt to contract it from the left usingleft_idx. The contraction potentially occurs each time we expand, but each character in thelarge_stringis considered at most twice (once for expansion and once for contraction). Therefore, the contraction does not exceed O(N) across the entirety of the algorithm. The most we can do is iterating the entirelarge_stringtwice, which implies O(N) time.
- Expanding the Window: We iterate through each character in the
Given that these operations are sequential and not nested, the total time complexity is O(M) for the initial setup and O(N) for processing the
large_string, leading to a combined complexity of O(N + M). -
-
Space Complexity: O(N + M). The space complexity is mainly influenced by the storage required for two dictionaries (
target_char_countsandsubstr_char_counts) and the substring bounds.Explanation:
-
Character Count Dictionaries
- The
target_char_countsdictionary's size is proportional to the number of unique characters intarget_string, which in the worst case could be as large as M. Thesubstr_char_countsdictionary stores counts of characters as they appear in the current window oflarge_string. In the worst case (wherelarge_stringcontains all characters oftarget_stringpossibly multiple times), this dictionary could grow to size proportional to N.
- The
-
Tracking Substring Bounds
- The
smallest_substr_intervaluses constant space to store the start and end indices of the smallest valid substring.
- The
Therefore, the maximum space used by the dictionaries is for the characters from both
target_stringand those counted inlarge_string, yielding a space complexity of O(N + M). -
Below is our coding solution in line with the intuitive walkthrough provided above:
from collections import Counter, defaultdict
# O(n + m) time | O(n + m) space
def find_smallest_substr_containing_target(large_string, target_string):
# Our target char count dictionary:
# target_string = "aabcc&" => {'a': 2, 'b': 1, 'c': 2, '&': 1}
target_char_counts = Counter(target_string)
# How many unique chars in the target string have we fully found so far?
unique_target_chars_hit = 0
# The left and right indices of the smallest substring containing all the
# chars in 'target_string'.
smallest_substr_interval = [float("-inf"), float("inf")]
# Current substring's char counts.
substr_char_counts = defaultdict(lambda: 0)
left_idx, right_idx = 0, 0
# 'right_idx' will be shifted to the right until it includes all the required
# characters from the 'target_string', accounting for their frequency as they
# appear in the target_string.
while right_idx < len(large_string):
right_char = large_string[right_idx]
# If the encountered char is not a target char, we simply continue.
if right_char not in target_char_counts:
right_idx += 1
continue
# We have encountered a target char. Increment its count in our dictionary.
substr_char_counts[right_char] += 1
# If we encountered the target char enough times, mark it as fulfilled!
if substr_char_counts[right_char] == target_char_counts[right_char]:
unique_target_chars_hit += 1
# We move the 'left_idx' to the right until the substring between 'left_idx' and
# 'right_idx' no longer contains a sufficient number of the required target chars.
# The purpose of this is to find the smallest substring that contains all the target
# chars (each at least as frequent as they appear in the 'target_string').
# e.g., target_string = "aabcc&" => len(target_char_counts) = 4.
while left_idx <= right_idx and unique_target_chars_hit == len(target_char_counts):
# Is the candidate substring the smallest one we ever found?
smallest_substr_interval = find_smallest_interval(smallest_substr_interval, left_idx, right_idx)
left_char = large_string[left_idx]
# The encountered char is a target char. Thus, we need to decrease its frequency.
if left_char in target_char_counts:
substr_char_counts[left_char] -= 1
# The char count may go below its frequency in the 'target_string'.
# In which case, we would need to decrement the 'unique_target_chars_hit'.
if substr_char_counts[left_char] < target_char_counts[left_char]:
unique_target_chars_hit -= 1
left_idx += 1
right_idx += 1
# Return the smallest substring if there is one.
if smallest_substr_interval[0] == float("-inf"): return ""
return large_string[smallest_substr_interval[0] : smallest_substr_interval[1] + 1]
# O(1) time | O(1) space.
# Helper method to compare a candidate substring with the current smallest substring.
def find_smallest_interval(curr_substr_interval, left_idx, right_idx):
if curr_substr_interval[1] - curr_substr_interval[0] < right_idx - left_idx:
return curr_substr_interval
return [left_idx, right_idx]
Final Notes
We believe this question has been asked frequently by Apple in recent interviews! It exemplifies the kind of optimization and problem-solving challenges common in the tech industry, particularly valued by Apple.
We believe this question has been asked frequently by Apple, making it very important for any candidate preparing for an interview with Apple soon. Here are some insights and strategies to consider for this particular problem:
1. Sliding Window Technique: The sliding window technique is central to our approach. It involves maintaining a window in the large_string that can expand or contract based on the presence of the required characters from the target_string. Understanding and applying the sliding window technique is essential. At Apple, where processing efficiency can significantly impact user experience and system performance, being proficient with such algorithms is crucial.
- Expanding the Window: We use a right pointer,
right_idx, which scans through thelarge_stringfrom left to right. As it moves, it includes characters in the current window and checks if they are part of thetarget_string. If they are, their counts are adjusted in a tracking dictionary. - Contracting the Window: Once the window contains all the necessary characters, the left pointer,
left_idx, starts moving right to minimize the window size while still containing all the necessary characters. This step ensures that we find the smallest possible substring that fulfills the criteria.
2. Two-Pointer Approach: Our solution employs two pointers to manage the window's boundaries effectively. The two-pointer approach is commonly used and highly valued by Apple interviewers.
- Right Pointer (right_idx): It is responsible for expanding the window to include new characters and increase the potential substring size.
- Left Pointer (left_idx): It manages the contraction of the window. This pointer moves right only when the current window has all the target characters, aiming to reduce the window size to the minimal necessary length.
The two-pointer approach is a crucial technique in algorithm design, favored for its efficiency in handling arrays and strings by minimizing complexity without extra memory use. This method is frequently emphasized in Apple interviews, highlighting a candidate's ability to optimize solutions effectively.
3. Optimization and Efficiency: The two-pointer approach in this problem underlines the importance of writing optimized code that performs well under constraints, a vital skill in Apple's software development.
4. Practical Application: Show how this approach can be applied in real-world software problems, such as optimizing data processing or improving the efficiency of feature implementations in iOS environments.
5. Complexity Analysis: Discussing the efficiency of your approach compared to brute force methods is particularly relevant at Apple. It showcases your ability to enhance algorithm performance and efficiency, skills highly valued in Apple's innovative technology landscape.
6. Scalable Solutions: Apple's vast ecosystem requires scalable solutions that perform efficiently on a large scale. Highlighting how your solution can be adapted and scaled for different applications or larger datasets can be a significant plus.
7. Clear Communication of Solutions: Apple values clarity in communication, especially of complex solutions. Demonstrating your ability to clearly explain your thought process and solution can set you apart in the interview process.
8. Relevance to Apple's Context: Tie your solution to potential real-world applications within Apple's ecosystem, showing an understanding of where and how such an optimization problem could directly impact Apple's products and services.
Preparing for a role at Apple means showcasing not just technical expertise but also the ability to apply these skills to solve practical, impactful problems. Remember, your ability to translate theoretical knowledge into real-world applications is highly prized, especially in a company at the cutting edge of technology like Apple.
Keep pushing forward, and good luck!

