Q1 - Product Development Order
We believe this interview question has recently been asked by Apple for full-time software engineers at junior positions.
Imagine you are organizing a complex product development process at Apple, where each step in the process is labeled from 0 to numSteps - 1. You are provided with
an array dependencies where
dependencies[i] = [a, b] indicates that step b must be completed before step a.
For example, the pair [0, 1] means that to start step 0, step 1 must be finished first. Your goal is to determine the sequence in which the steps should be
performed to complete the entire product development process. If there are multiple valid sequences, return any of them. If it is impossible to complete all steps
due to circular dependencies, return an empty array.
Example 1
Input:
num_steps = 6
dependencies = [[1, 0], [2, 0], [3, 1], [3, 2], [2, 4], [1, 5]]
Output:
[0, 4, 5, 2, 1, 3] is one of the possible solutions.
Example 2
Input:
num_steps = 2
dependencies = [[1, 0]]
Output:
[0, 1]
Example 3
Input:
num_steps = 2
dependencies = [[0, 1], [1, 0]]
Output:
[] since it is not possible to finish all the steps due to a circular dependency.
Solution
In this problem, we need to determine the sequence in which steps in a complex product development process should be performed. Each step depends on the completion of other steps, and our goal is to find a valid order of steps or determine if it's impossible due to circular dependencies.
To solve this problem, we'll use Topological Sorting which is commonly used to determine the linear ordering of vertices in a Directed Acyclic Graph (DAG). Let's break down the solution step by step.
1) Understanding the Problem
When you look at this problem, it appears to be a graph problem where each step is a node, and each dependency is a directed edge. The dependencies indicate the direction of the edges.
The problem requires finding an ordering of steps such that for every directed edge u -> v, step u comes before step v.
The topological sorting technique is appropriate here because it ensures that the directed edges follow the specified order, helping us find a valid sequence of steps. For instance, consider the Example-1:
Example 1
Input:
num_steps = 6
dependencies = [[1, 0], [2, 0], [3, 1], [3, 2], [2, 4], [1, 5]]
Output:
[0, 4, 5, 2, 1, 3] is one of the possible solutions.
Here, the dependency array is: dependencies = [[1, 0], [2, 0], [3, 1], [3, 2], [2, 4], [1, 5]]. How can we represent these dependencies as a graph? In other words, how can we translate
this into a graph problem? Take a look at the graph below. The graph visually illustrates how each step is interconnected and dependent on one another:
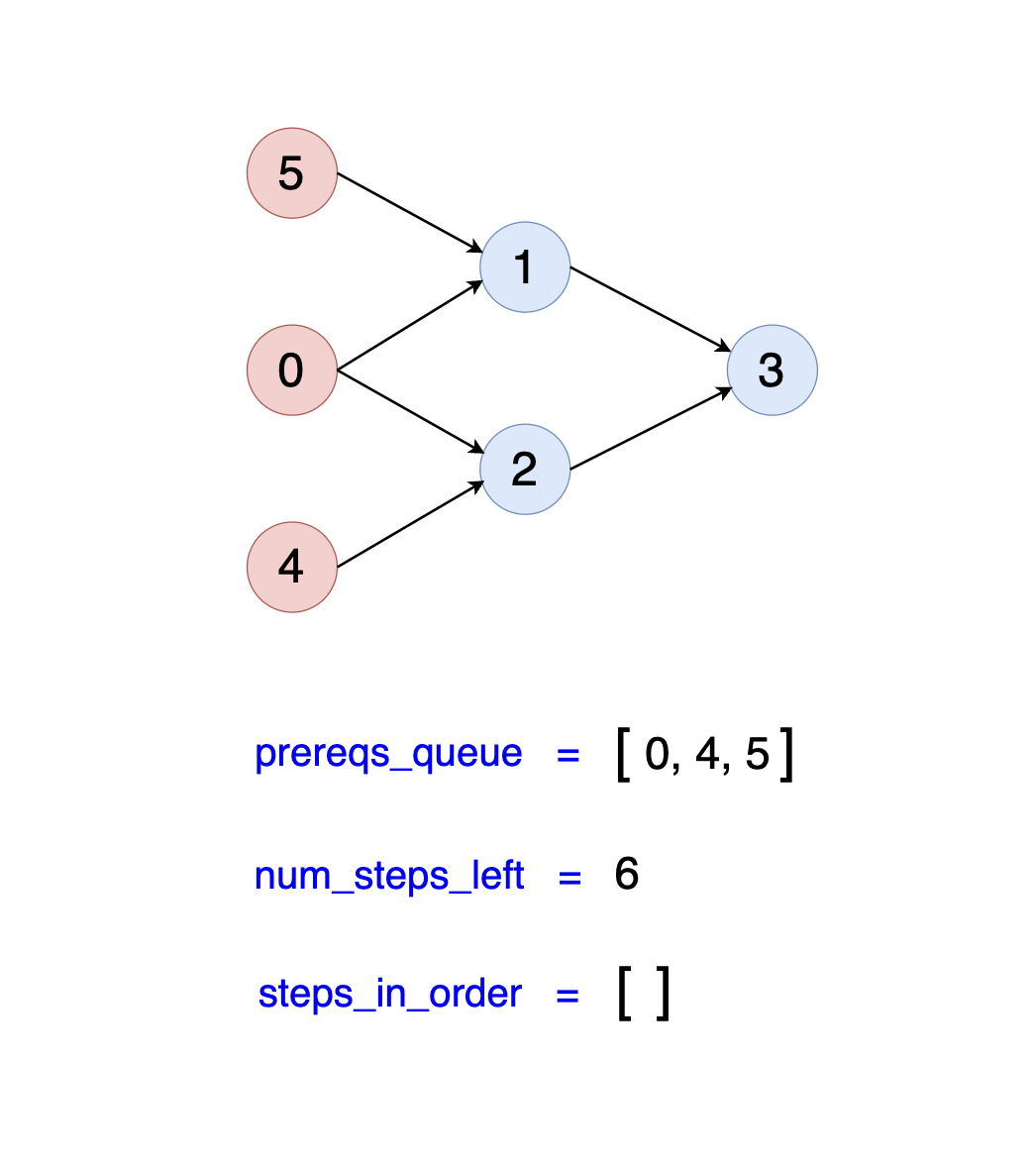
Notice that steps 0, 4, and 5 are initial steps that can be performed immediately as they do not have any prerequisites.
Additionally, observe that step 3 must be the final step since all other steps lead to it.
To gain a clearer visualization of how the algorithm functions, please refer to the
Visual Demonstration of Example-1 section at the bottom of this page.
2) Initializing Necessary Variables
First, we initialize some variables to store the prerequisites and the in-degrees of each step:
In-degrees: In the context of a graph, the in-degree of a node represents the number of edges coming into that node. In this problem, the in-degree of a step indicates the number of other steps that must be completed before this step can begin (e.g., the number of prerequisites that a step has).
Initial Setup
from collections import defaultdict, deque
# O(V + E) time | O(V + E) space
def find_product_development_order(num_steps, dependencies):
# Dictionary that maps a previous step to a list of next steps that require
# the previous step to be finished first. For instance,
# if step 0 is a prerequisite for steps 2, 4, 5, then: {0 -> [2, 4, 5]}
prereq_to_next_steps = defaultdict(list)
# Dictionary that maps a step to its number of prerequisites.
# If step 5 has 3 prerequisites, then: {5 -> 3}
in_degrees = defaultdict(lambda: 0)
# Final result.
steps_in_order = []
...
-
Here,
prereq_to_next_stepsis a dictionary that maps a step to the list of steps that depend on it. For example, if step0is a prerequisite for steps2and3, the dictionary will have an entry like{0: [2, 3]}. This helps us track which steps are dependent on the completion of a given step. -
in_degreesis another dictionary that keeps track of how many prerequisites each step has. For example, if step1has two prerequisites, the dictionary will have an entry like{1: 2}. This helps us understand how many other steps need to be completed before a given step can be started. -
steps_in_orderwill store the final sequence of steps that satisfies all the dependencies. It will be built as we process each step, ensuring that all prerequisites for a given step are completed before the step itself is added to the sequence.
3) Building the Graph
Next, we build the graph by populating the prereq_to_next_steps and in_degrees dictionaries based on the dependencies provided. Let's look at the graph representing Example-1 once again:

-
Let's consider step 0:
- Since step
0is a prerequisite for steps1and2, ourprereq_to_next_stepsdictionary will contain
{0: [1, 2]}. - Step
0has no prerequisites itself, so it has no in-degrees:in_degrees[0] = 0.
- Since step
-
Let's now consider step 1:
- Since step
1is a prerequisite for step3only, ourprereq_to_next_stepsdictionary will have{1: [3]}. - Step
1has two prerequisites (steps0and5), soin_degrees[1] = 2.
- Since step
This same process applies to the other steps, constructing the prereq_to_next_steps and in_degrees mappings accordingly.
Below is the code snippet responsible for populating the prereq_to_next_steps and in_degrees dictionaries based on the provided dependencies:
Building The Graph Represented By The Two Dictionaries
# Construct both dictionaries.
for dependency_pair in dependencies:
prereq, step = dependency_pair[1], dependency_pair[0]
prereq_to_next_steps[prereq].append(step)
in_degrees[step] += 1 # increment step's number of prereqs.
Again, for each dependency pair [a, b], we update prereq_to_next_steps to show that b is a prerequisite for a, and we increment the in-degree of a because it has one more prerequisite.
Keeping track of in-degrees is crucial because it helps us identify steps that can be performed immediately, e.g., steps with an in-degree of zero. We'll come back to this concept very soon.
4) Finding Initial Prerequisites
To begin processing the steps, we need to identify the steps that have no prerequisites and add them to our processing queue. These are the steps that can be executed immediately without waiting for any other steps to be completed first. But how do we find these initial prerequisites? That's where the in-degrees dictionary comes to the rescue! The in-degrees dictionary keeps track of the current set of prerequisites at each level, making it easy to find steps that can be started right away.
If the in-degrees of a step (e.g., in_degrees['a'] = 0) is zero, that means there is no node pointing to it, namely it has no prerequisites.
We use a helper function, construct_prereqs_queue, to initialize this queue:
Construction Of Our Prereqs Queue With The Initial Prerequisites
# Our prerequisites queue containing the initial prerequisites.
prereqs_queue = construct_prereqs_queue(num_steps, in_degrees)
# Helper function to find the initial prerequisites.
def construct_prereqs_queue(num_steps, in_degrees):
prereqs_queue = deque()
for s in range(num_steps):
if s not in in_degrees:
prereqs_queue.append(s)
return prereqs_queue
This function iterates through all the steps and adds those with an in-degree of zero (i.e., no prerequisites) to the queue.
Why use a Queue: A queue is an ideal data structure for this purpose because it follows the First-In-First-Out (FIFO) principle. This ensures that steps with no prerequisites are processed first, allowing subsequent steps that depend on them to be processed in the correct order.
By using a queue, we can efficiently manage the order of processing steps. When we add steps with no prerequisites to the queue initially, we ensure that they are processed first. As we process each step, we can then add new steps to the queue as their prerequisites are completed. This approach allows us to maintain a clear and logical sequence for processing all steps, ensuring that dependencies are respected and the overall process is efficient.
In summary, the queue helps us manage the order of execution by always processing the steps with no prerequisites first and then adding steps to the queue as their prerequisites are fulfilled. This ensures that we can complete all steps in the correct sequence, respecting all dependencies.

You can see in the above image corresponding to Example-1 that the red circled nodes (representing development steps) are the initial steps that need to be taken, as they have no prerequisites.
These steps are identified as the starting points because there are no dependencies blocking their execution. The construct_prereqs_queue(num_steps, in_degrees) function scans through
all steps and selects those with an in-degree of zero, meaning they have no prerequisites. As a result, our initial prerequisite queue would be: prereqs_queue = [0, 4, 5].
These are the steps we can begin working on immediately, ensuring the process starts without delays.
5) Processing the Queue
Now, we process the queue using a Breadth-First Search (BFS) approach. This ensures that we process each step only after all its prerequisites have been processed:
BFS Traversal To Discover New Prerequisites
while prereqs_queue:
prereq = prereqs_queue.popleft()
steps_in_order.append(prereq)
num_steps -= 1 # We took the prerequisite, so decrement the num of steps.
# All the steps that have the current prerequisite as a requirement:
for step in prereq_to_next_steps[prereq]:
in_degrees[step] -= 1 # We took one of its prerequisites.
# The step itself became a prerequisite, so add it to the queue.
if in_degrees[step] == 0:
prereqs_queue.append(step)
In this part, we:
- Dequeue a step with no prerequisites: We start by removing a step from the front of the queue. This step is guaranteed to have no remaining prerequisites because of how we constructed our initial queue.
- Append it to the
steps_in_orderlist: This step is then added to our final list of steps in the order they should be executed. - Decrement
num_steps: Since we have successfully processed one step, we decrease the total number of steps left to process by one. - For each step dependent on the current step, decrement its
in-degree: We look at all the steps that rely on the current step being completed. For each of these dependent steps, we reduce its in-degree by one, signifying that one of its prerequisites has been met. - If a step's
in-degreebecomes zero, add it to the queue: When a step's in-degree reaches zero, it means all its prerequisites have been satisfied, and it can now be processed. We then add this step to the queue so it can be executed in subsequent iterations.
This process continues until there are no more steps left in the queue.
Observe the diagrams below. Notice that we dequeue the first item in the queue, which is step 0. Since step 0 has no remaining prerequisites, it is eligible to be performed,
so we add it to our steps_in_order list. Step 0 is a prerequisite for steps 1 and 2. After performing step 0, we can consider steps 1 and 2 for execution.
This process involves "removing" the edges from step 0 to steps 1 and 2 in the graph, which corresponds to decrementing the in-degree values of steps 1 and 2. The diagram below demonstrates
this process:
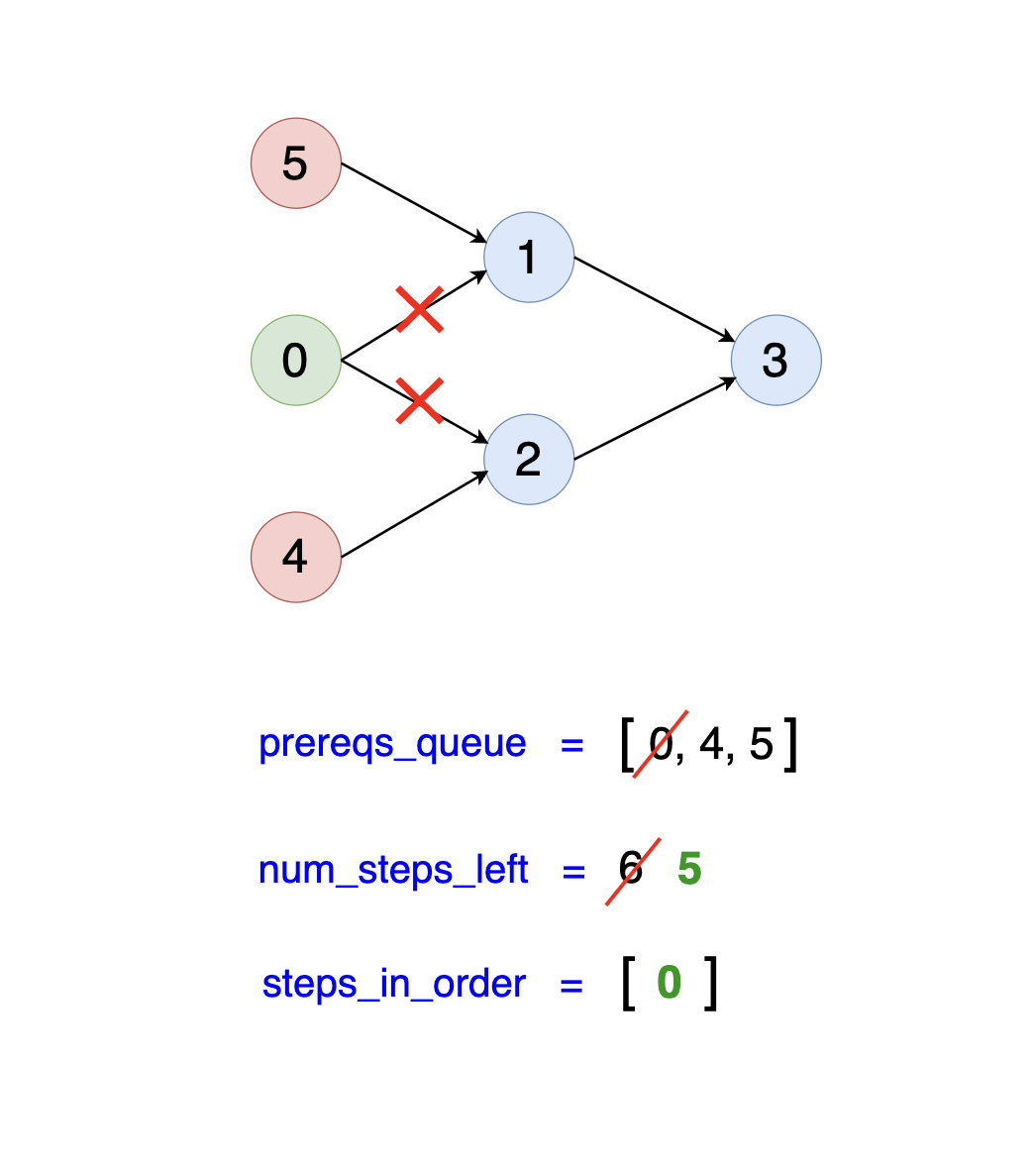
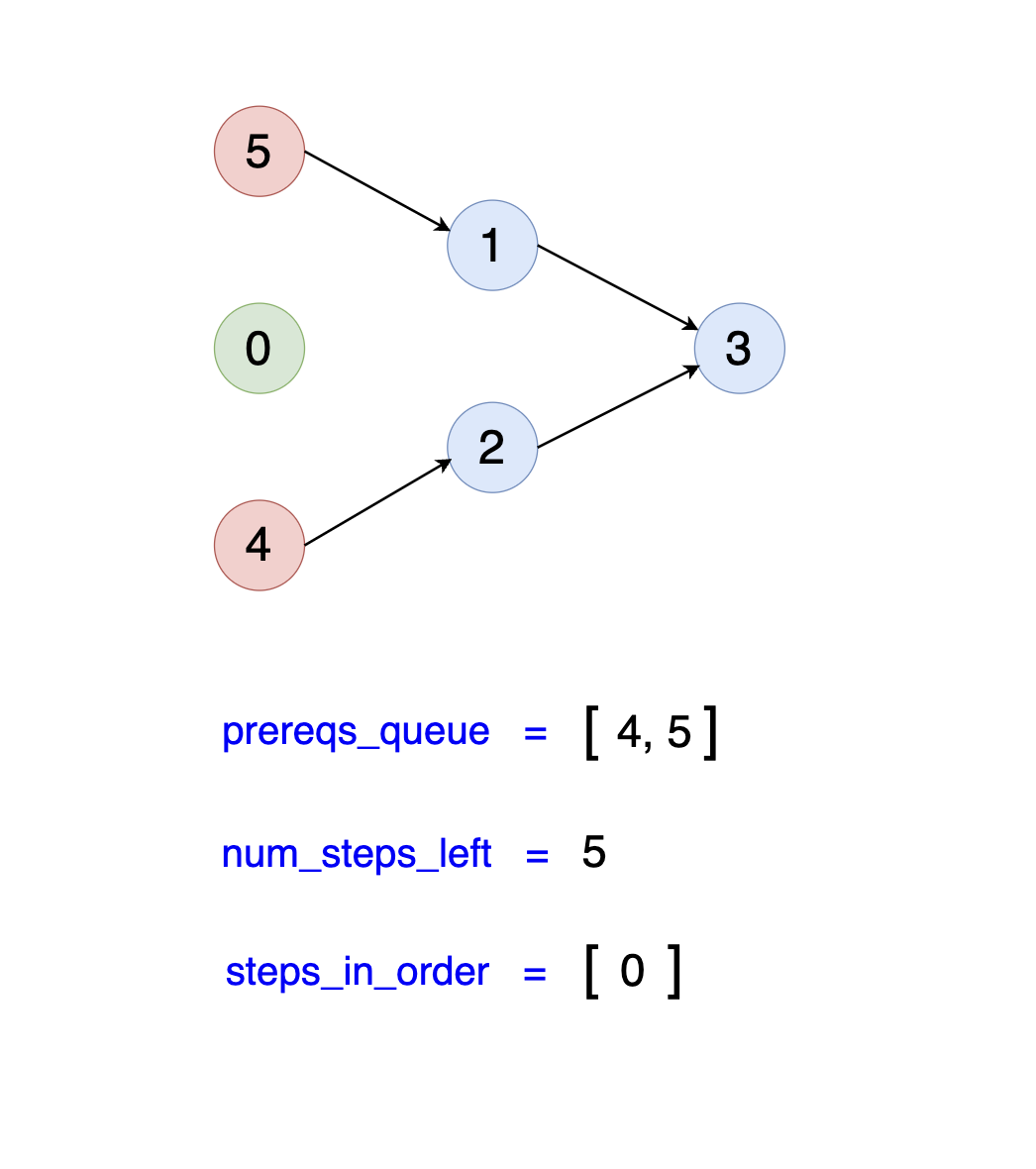
As you can see, both steps 1 and 2 now have one less prerequisite (e.g., one less in-degree). However, they still have one more prerequisite
each: step 1 requires step 5, and step 2 requires step 4. Thus, they have not yet become prerequisites themselves, so we cannot add them to our prereqs_queue yet.
This process is represented by the code snippet below:
Discovering New Prerequisites
in_degrees[step] -= 1 # We took one of its prerequisites.
# If the step itself became a prerequisite, we add it to the queue.
if in_degrees[step] == 0:
prereqs_queue.append(step)
For instance, after a few iterations, we will perform step 4 (the only remaining prerequisite of step 2), which will make step 2 a prerequisite itself, as all its prerequisites
will have already been performed. This is shown below:
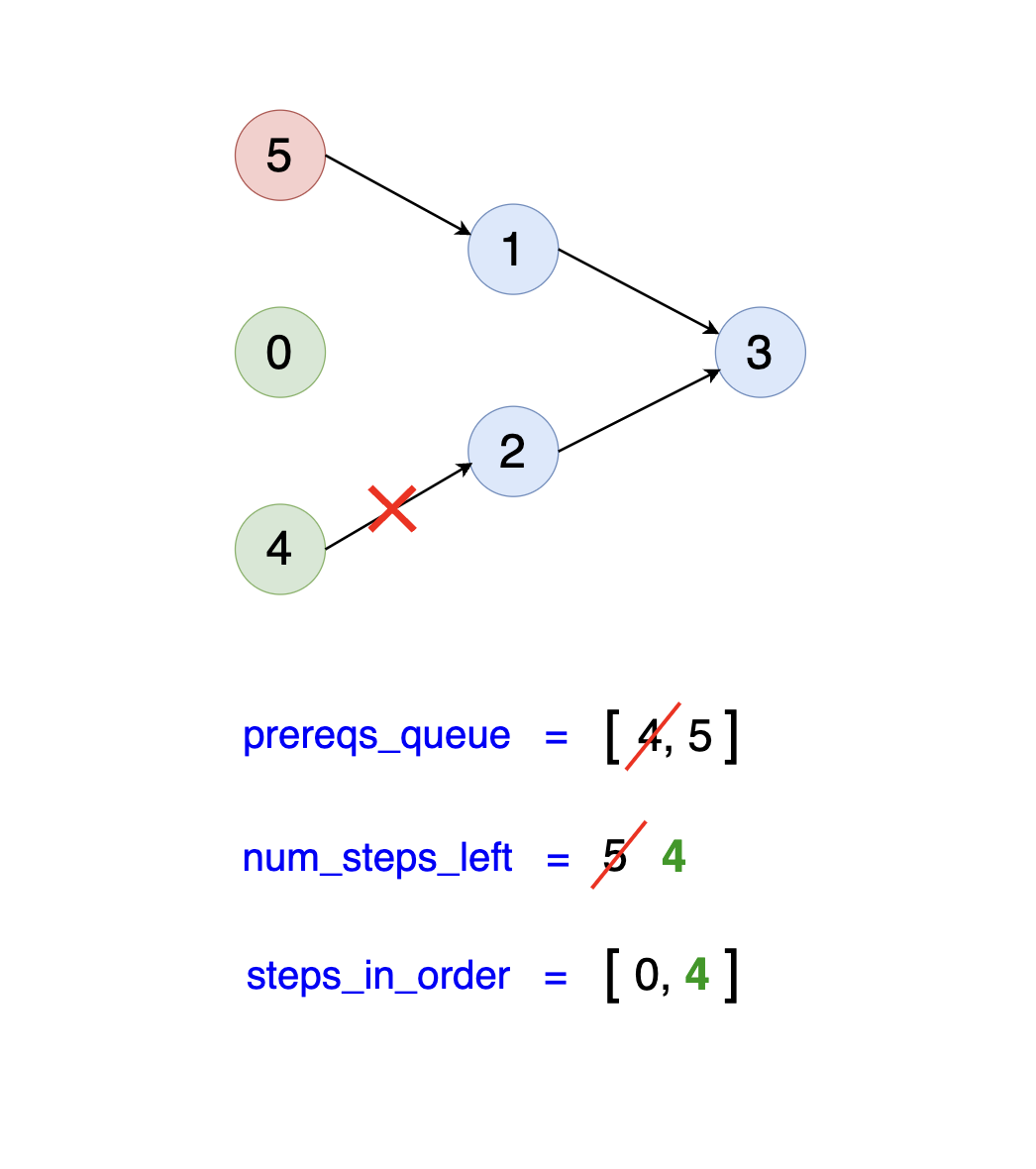
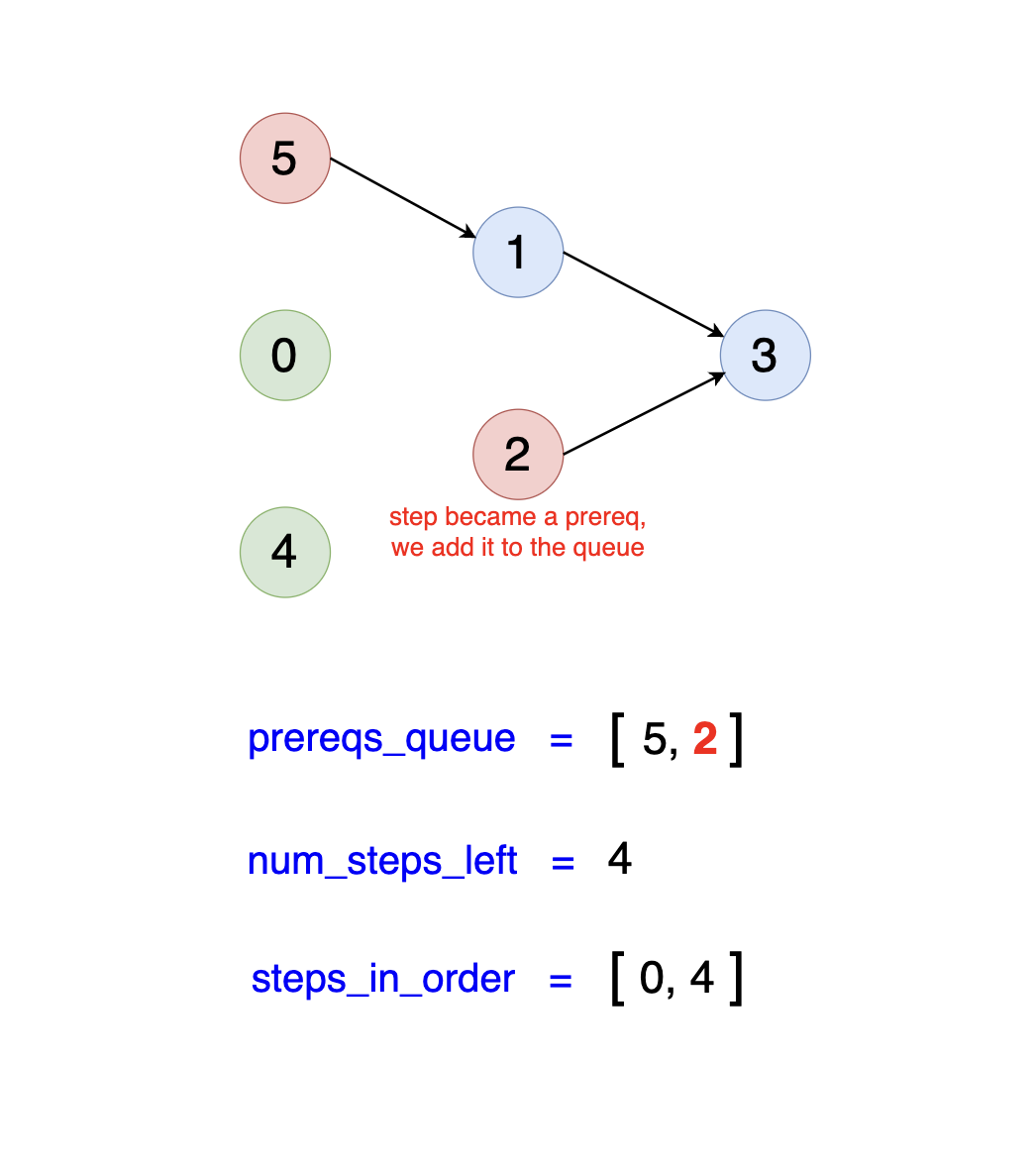
6) Checking Completion
Finally, we check if we were able to process all the steps:
Checking Whether All the Steps Were Processed
# Only return if we were able to complete all the steps.
return steps_in_order if num_steps == 0 else []
If num_steps is zero, it means we've processed all steps successfully and return the order. If not, we return an empty list indicating it's impossible to complete all steps due to
circular dependencies.
Complexity Analysis
-
Time Complexity: O(V + E), where V represents the number of steps (vertices) and E represents the number of dependencies (edges).
Explanation:
-
Building the Graph and In-Degree Dictionary
- Constructing the
prereq_to_next_stepsdictionary and thein_degreesdictionary requires iterating through each dependency pair once. This takes O(E) time.
- Constructing the
-
Initializing the Queue with Initial Prerequisites
- Finding the initial prerequisites involves checking the in-degrees of all V steps, which takes O(V) time.
-
Processing the Steps
- Each step is processed exactly once, and for each step, we may check all its outgoing edges (next steps). This takes O(V + E) time.
Combining these steps, the overall time complexity is O(V + E), which is efficient for this problem.
-
-
Space Complexity: O(V + E). The space complexity is mainly influenced by the storage requirements of the graph representation and the in-degree dictionary.
Explanation:
-
Graph Representation
- The
prereq_to_next_stepsdictionary stores each step and its list of next steps, which in the worst case takes O(E) space.
- The
-
In-Degree Dictionary
- The
in_degreesdictionary stores each step and its count of prerequisites, taking O(V) space.
- The
-
Queue and Result Storage
- The
prereqs_queueandsteps_in_orderlists each require O(V) space.
- The
Therefore, the overall space complexity is O(V + E), accommodating the necessary data structures for efficient processing.
-
Visual Demonstration of the Algorithm
Below, we provide a step-by-step visual demonstration of Example-1. Each image corresponds to a specific iteration, illustrating the progression of the algorithm's operation.

Below is the coding solution for the algorithm we've just explored:
from collections import defaultdict, deque
# O(V + E) time | O(V + E) space
def find_product_development_order(num_steps, dependencies):
# Dictionary that maps a previous step to a list of next steps that require
# the previous step to be finished first. For instance,
# if step 0 is a prerequisite for steps 2, 4, 5, then: {0 -> [2, 4, 5]}
prereq_to_next_steps = defaultdict(list)
# Dictionary that maps a step to its number of prerequisites.
# If step 5 has 3 prerequisites, then: {5 -> 3}
in_degrees = defaultdict(lambda: 0)
# Final result.
steps_in_order = []
# Construct both dictionaries.
for dependency_pair in dependencies:
prereq, step = dependency_pair[1], dependency_pair[0]
prereq_to_next_steps[prereq].append(step)
in_degrees[step] += 1 # increment step's number of prereqs.
# Our prerequisites queue containing the initial prerequisites.
prereqs_queue = construct_prereqs_queue(num_steps, in_degrees)
while prereqs_queue:
prereq = prereqs_queue.popleft()
steps_in_order.append(prereq)
num_steps -= 1 # We took the prerequisite, so decrement the num of steps.
# All the steps that have the current prerequisite as a requirement:
for step in prereq_to_next_steps[prereq]:
in_degrees[step] -= 1 # We took one of its prerequisites.
# The step itself became a prerequisite, so add it to the queue.
if in_degrees[step] == 0:
prereqs_queue.append(step)
# Only return if we were able to complete all the steps.
return steps_in_order if num_steps == 0 else []
# Helper function to find the initial prerequisites.
def construct_prereqs_queue(num_steps, in_degrees):
prereqs_queue = deque()
for s in range(num_steps):
if s not in in_degrees:
prereqs_queue.append(s)
return prereqs_queue
Final Notes
We believe the "Product Development Order" problem has appeared frequently in recent interviews for software engineers at Apple. This problem tests a candidate's ability to address complex graph-based issues, particularly those involving dependencies and ordering.
Here are some key takeaways to consider:
1. Understand the Problem Requirements:
- Ensure you grasp the constraints and the goal of the problem clearly.
- The problem involves determining an order to complete steps in a product development process, considering dependencies.
2. Think in Terms of Graphs:
- Visualize the steps as nodes in a graph and the dependencies as directed edges.
- The problem becomes one of finding a valid topological ordering of a Directed Acyclic Graph (DAG).
3. Implement Topological Sorting Effectively:
- Use topological sorting to ensure the steps are performed in the correct order.
- Utilize a queue to manage the BFS traversal and ensure that nodes are processed in the correct sequence.
4. Optimize Your Solution:
- Ensure the solution has a time complexity of O(V + E), where V is the number of steps and E is the number of dependencies.
- Aim for a space complexity of O(V + E), which accommodates the graph representation and the queue.
5. Handle Edge Cases:
- Consider scenarios where it is impossible to complete all steps due to circular dependencies.
- Make sure your solution handles small graphs, large graphs, and graphs with varying distributions of dependencies.
6. Communicate Your Thought Process:
- During the interview, clearly explain why you chose topological sorting and how you are managing the traversal.
- Discuss any edge cases and how your solution addresses them.
7. Test Thoroughly:
- Validate your solution with multiple test cases, including edge cases, to ensure its correctness.
- Demonstrate the robustness of your solution by explaining the test cases to your interviewer.
By mastering these concepts and practicing the implementation, you'll be well-prepared to tackle Apple's "Product Development Order" interview question with confidence. Good luck, and remember that clear communication and practice are key to success!

