Q2 - Min Number of Minutes to Fix All Packages

Imagine you are managing a large Amazon warehouse where you have implemented a new recovery protocol to ensure all packages are in good condition. Each package in the warehouse is scanned and classified into a grid system based on its condition. In this grid:

• 0 represents an empty cell.
• 1 represents a package in good condition.
• -1 represents a package that is damaged and needs recovery.

Every minute, a warehouse worker checks and works near packages in good condition (1). Any damaged package (-1) that is adjacent (up, down, left, or right) to a package in good condition (1) becomes recovered and turns into good condition due to the worker's efforts. Your goal is to determine the minimum number of minutes required for all packages to become good. If it is impossible to achieve this state, return -1.

For instance, consider Example-1:

 [[1, -1, -1],
  [-1, 0, -1],
  [-1, 0, -1]]

 [[1, 1, -1],
  [1, 0, -1],
  [-1,0, -1]]

 [[1, 1, 1],
  [1, 0, -1],
  [1, 0, -1]]

 [[1, 1, 1],
  [1, 0, 1],
  [1, 0, -1]]

 [[1,  1,  1],
  [1,  0,  1],
  [1,  0,  1]]

Since it required 4 iterations to convert all the packages to good condition, we return 4 minutes as the output.

Your task is to write a function that takes the grid as input and returns the minimum number of minutes required for all packages to become good. Again, the function should return -1 if it's not possible.

Input:
 [[1, -1, -1],
  [-1, 0, -1],
  [-1, 0, -1]]

Output:
4 minutes

Input:
 [[1, 0]]

Output:
0 minutes (since there is only one package and it's already in good condition).

Input:
 [[1, 0],
  [0, -1]]

Output:
-1
Since it is impossible for the damaged package at position (1, 1) to become good.
The initial good package at position (0, 0) cannot influence the damaged package at (1, 1) 
due to the lack of adjacent connection through cells that can change state.

Solution

To solve this problem, we'll use a Breadth-First Search (BFS) approach. But why BFS? Let's break down the intuition behind this choice.

When you look at the problem, you'll notice an iterative nature where we can only discover new branches (in our case, damaged packages that can be recovered) from already discovered nodes (good condition packages). This iterative process of discovering new nodes from previously discovered nodes is a hallmark of graph traversal problems.

Our goal is to find the shortest path from all initially good packages to convert all damaged packages. This is essentially a shortest-path problem in an unweighted graph, where we want to minimize the time (or distance) taken to convert all packages.

BFS is particularly suitable for this kind of problem because:

• BFS explores all possible moves level by level, ensuring that we find the shortest path in an unweighted grid.
• It processes nodes in layers, making it ideal for situations where we want to explore all neighbors of a node before moving on to the next level. This aligns perfectly with our requirement to convert packages iteratively minute by minute. Now it makes sense right?

With this understanding, let's dive into the implementation details.

1) Initialize Variables

Before we can begin the process of converting all the damaged packages to good condition, we need to perform some initial setup. This involves identifying the positions of all the good packages and counting the total number of bad packages. This step is crucial because it provides the starting point for our Breadth-First Search (BFS) algorithm. Let's break down this process further.

We start by initializing several important variables:

• rows and cols to store the dimensions of the grid.
• directions to define the possible movements (up, down, left, right) from a given cell.
• good_packages, a queue to keep track of all the positions of good packages.
• num_bad_packages to count the total number of bad packages.
• minutes to keep track of the time required to convert all packages to good condition.

rows, cols = len(grid), len(grid[0])
directions = [[-1, 0], [1, 0], [0, 1], [0, -1]]
# Queue that contains the location of each good package.
good_packages = deque()
# To keep track of the number of bad packages.
num_bad_packages = 0
# Minimum amount of minutes required to fix all packages.
minutes = 0

2) Locate All Initially Good Packages and Count Bad Packages

We iterate through each cell in the grid to identify the initial state:

• If the cell contains a 1, it means there is a package in good condition. We append its position to the good_packages queue because this will be our starting point for the BFS.
• If the cell contains a -1, it indicates a damaged package. We increment the num_bad_packages counter.

# 1) Locate all initially good packages.
# 2) Find the total number of bad packages.
for r in range(rows):
    for c in range(cols):
        if grid[r][c] == 1:
            good_packages.append([r, c])
        elif grid[r][c] == -1:
            num_bad_packages += 1

Below is a visual representation of this process for Example-1:

3) Add a Dummy Position to Separate Each Iteration

  # To separate each iteration (e.g., each minute),
  # we are adding a dummy position to our queue.
  good_packages.append([-1, -1])

When using Breadth-First Search (BFS) to solve this problem, we need to ensure that we correctly count the number of iterations (minutes) required to convert all damaged packages to good condition. One effective way to manage this is by using a dummy position in our queue. Let's delve into why and how we do this:

Purpose of the Dummy Position: The BFS algorithm explores nodes level by level. In the context of this problem, each level corresponds to one minute of recovery time. However, the BFS algorithm itself doesn't inherently keep track of the levels or iterations. By adding a dummy position [-1, -1] to our queue, we create a marker that indicates the end of one level and the beginning of another. This helps us increment the minutes counter accurately.

4) Processing the Queue (BFS)

The core of the solution lies in the Breadth-First Search (BFS) traversal of the grid, which is handled by a queue. Let's break down the queue processing step by step:

Initial Setup:
Again, we start by initializing the queue good_packages with the positions of all initially good packages and a dummy position [-1, -1] to separate iterations. This setup ensures we can accurately track the time (in minutes) taken to convert all bad packages to good ones.

while good_packages:
    row, col = good_packages.popleft()
    # This suggests that we are starting a new iteration (e.g., next minute).
    if row == -1:
        minutes += 1
        # Otherwise infinite loop: [[-1, -1], [-1, -1]...]
        if good_packages:
            good_packages.append([-1, -1]) # To indicate a new iteration.
    # Explore from the current good package.
    else:
        for dir in directions:
            nbr_row, nbr_col = row + dir[0], col + dir[1]
            if is_valid_step(grid, rows, cols, nbr_row, nbr_col):
                # Bad package will become a good one.
                # We need to add this new good package into our queue.
                grid[nbr_row][nbr_col] = 1 # Package became good.
                good_packages.append([nbr_row, nbr_col])
                num_bad_packages -= 1 # Since it has just become a good one.

1. Processing Each Element in the Queue

row, col = good_packages.popleft()

• We use popleft() to dequeue the first element from good_packages.
• This element can either be a position of a good package or the dummy position [-1, -1].

The image below shows this process:

2. Handling the Dummy Position

# This suggests that we are starting a new iteration (e.g., next minute).
if row == -1:
    minutes += 1
    # Otherwise infinite loop: [[-1, -1], [-1, -1]...]
    if good_packages:
        good_packages.append([-1, -1]) # To indicate a new iteration.

• When row == -1, it indicates the start of a new iteration (minute).
• We increment the minutes counter because we've completed processing all packages for the current minute.
• If there are still packages in the queue added from the previous iterations, we add another dummy position to mark the end of the next minute.

Consider the example below, where we add an additional dummy position [-1, -1] at the end of Iteration 1:

3. Exploring from the Current Good Package

for dir in directions:
    nbr_row, nbr_col = row + dir[0], col + dir[1]
    if is_valid_step(grid, rows, cols, nbr_row, nbr_col):
        # Bad package will become a good one.
        # We need to add this new good package into our queue.
        grid[nbr_row][nbr_col] = 1 # Package became good.
        good_packages.append([nbr_row, nbr_col])
        num_bad_packages -= 1 # Since it has just become a good one.

• If the dequeued element is not the dummy position, it represents the coordinates of a good package.
• We use a for loop to explore all four possible directions (up, down, left, right) from the current package's position.

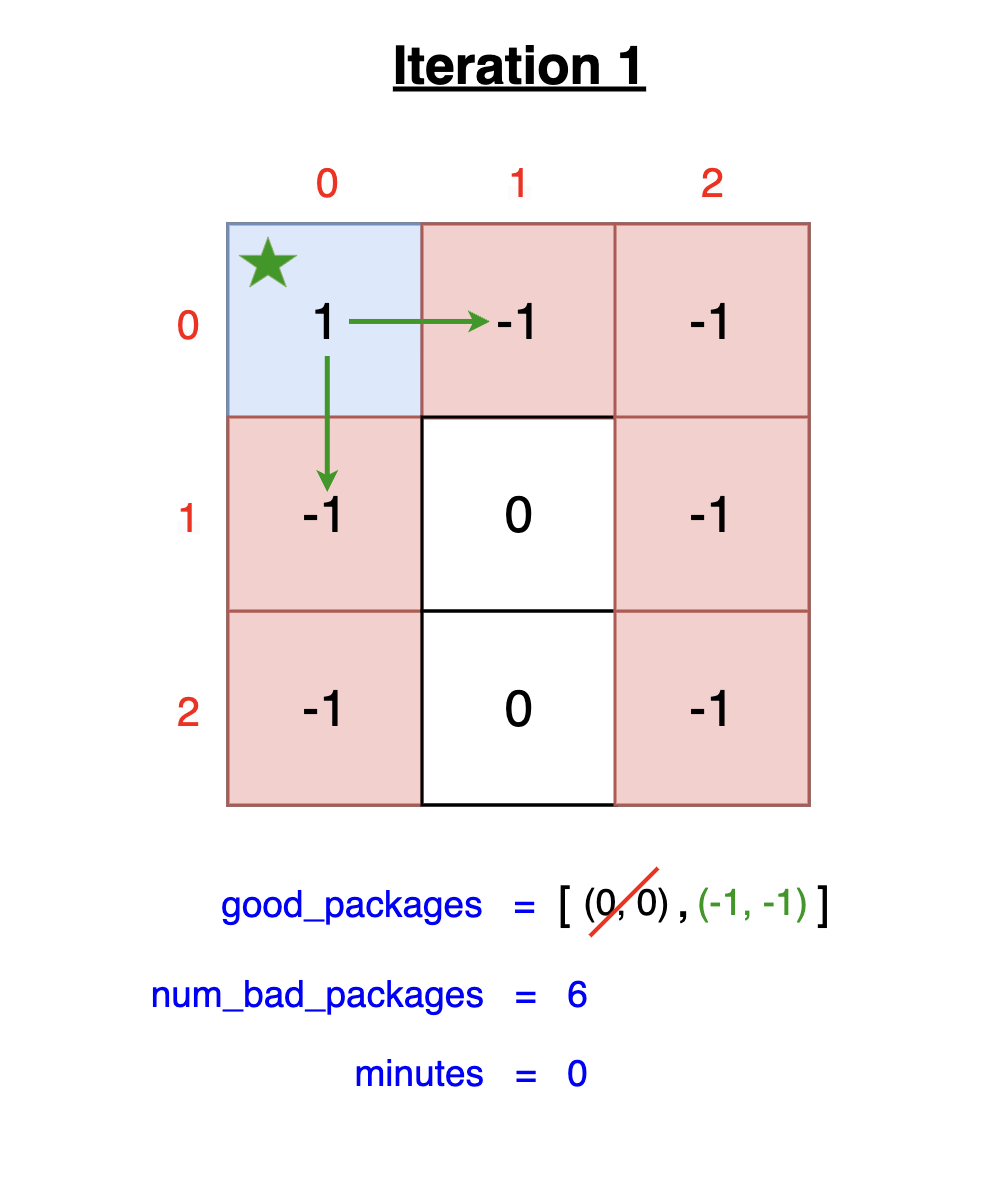
Below is an example where we explore bad packages from positions (0, 1) and (1, 0):

4. Checking Valid Steps

You can see from the above image that the only valid step for the position (0, 1) is right, and for the position (1, 0), it is down. Below, we will explain how this process works:

• For each direction, we calculate the neighboring cell's coordinates (nbr_row, nbr_col).

for dir in directions:
    nbr_row, nbr_col = row + dir[0], col + dir[1]
    if is_valid_step(grid, rows, cols, nbr_row, nbr_col):
        # Bad package will become a good one.
        # We need to add this new good package into our queue.
        grid[nbr_row][nbr_col] = 1 # Package became good.
        good_packages.append([nbr_row, nbr_col])
        num_bad_packages -= 1 # Since it has just become a good one.

• We call the is_valid_step() function to check if the neighboring cell is within the grid boundaries and if it contains a bad package (-1).

# Helper method to check if we are currently considering a bad package.
def is_valid_step(grid, rows, cols, r, c):
    return 0 <= r < rows and 0 <= c < cols and grid[r][c] == -1

5. Converting Bad Packages to Good

If the neighboring cell is a valid step, we:

• Change the cell's value from -1 to 1, indicating the package has been recovered and is now in good condition.
• Add the position of this newly recovered package to the queue, so it can be processed in subsequent iterations.
• Decrement the num_bad_packages counter because we have one less bad package to recover.

Below is the code snippet responsible for converting damaged packages into good ones within a single minute (or iteration):

if is_valid_step(grid, rows, cols, nbr_row, nbr_col):
    # Bad package will become a good one.
    # We need to add this new good package into our queue.
    grid[nbr_row][nbr_col] = 1 # Package became good.
    good_packages.append([nbr_row, nbr_col])
    num_bad_packages -= 1 # Since it has just become a good one.

Below, we provide a step-by-step visual demonstration of Example-1. Each image corresponds to a specific iteration, illustrating the progression of the algorithm's operation.

1 / 15

Complexity Analysis

• Time Complexity: O(r × c), where r represents the number of rows and c represents the number of columns in the grid.

  Explanation:

  1. Scanning the Grid

     • We iterate over each cell in the grid once to initialize the queue with good packages and count the bad packages. This operation is O(r × c).

  2. Breadth-First Search (BFS) Operation

     • In the worst-case scenario, every cell in the grid could be processed, and every cell could be added to the queue. Each cell is added to the queue and processed at most once, resulting in O(r × c) operations.

  Combining these parts, the overall time complexity of the algorithm is O(r × c).

• Space Complexity: O(r × c), where r represents the number of rows and c represents the number of columns in the grid.

  Explanation:

  1. Queue Storage

     • In the worst-case scenario, the queue could contain all the cells in the grid at once (e.g., all the packages are already in good condition), resulting in O(r × c) space.

  2. Grid Storage

     • The grid itself takes up O(r × c) space. This is not additional space since it's part of the input, but it is worth mentioning.

  Therefore, the overall space complexity is O(r × c).

Below is the coding solution for the algorithm we've just explored:

from collections import deque
def min_minutes_to_fix_packages(grid):
    rows, cols = len(grid), len(grid[0])
    directions = [[-1, 0], [1, 0], [0, 1], [0, -1]]
    # Queue that contains the location of each good package.
    good_packages = deque()
    # To keep track of the number of bad packages.
    num_bad_packages = 0
    # Minimum amount of minutes required to fix all packages.
    minutes = 0

    # 1) Locate all initially good packages.
    # 2) Find the total number of bad packages.
    for r in range(rows):
        for c in range(cols):
            if grid[r][c] == 1:
                good_packages.append([r, c])
            elif grid[r][c] == -1:
                num_bad_packages += 1
                
    # To separate each iteration (e.g., each minute),
    # we are adding a dummy position to our queue.
    good_packages.append([-1, -1])
    while good_packages:
        row, col = good_packages.popleft()
        # This suggests that we are starting a new iteration (e.g., next minute).
        if row == -1:
            minutes += 1
            # Otherwise infinite loop: [[-1, -1], [-1, -1]...]
            if good_packages:
                good_packages.append([-1, -1]) # To indicate a new iteration.
        # Explore from the current good package.
        else:
            for dir in directions:
                nbr_row, nbr_col = row + dir[0], col + dir[1]
                if is_valid_step(grid, rows, cols, nbr_row, nbr_col):
                    # Bad package will become a good one.
                    # We need to add this new good package into our queue.
                    grid[nbr_row][nbr_col] = 1 # Package became good.
                    good_packages.append([nbr_row, nbr_col])
                    num_bad_packages -= 1 # Since it has just become a good one.

    # If we were able to convert all bad packages into good ones, then return the min minutes.
    # Otherwise, it's not possible to do so. Return -1.
    return minutes - 1 if num_bad_packages == 0 else -1

# Helper method to check if we are currently considering a bad package.
def is_valid_step(grid, rows, cols, r, c):
    return 0 <= r < rows and 0 <= c < cols and grid[r][c] == -1

Final Notes

The "Min Number of Minutes to Fix All Packages" problem is a prime example of a challenge frequently posed in Amazon interviews. It tests a candidate's ability to implement graph traversal techniques and efficiently handle grid-based problems. Here are some key takeaways to consider:

1. Understand the Problem Requirements:

• Make sure to grasp the constraints and the goal of the problem clearly.
• The problem involves transforming all damaged packages (-1) into good packages (1) using an iterative process.

2. Think in Terms of Graphs:

• Visualize the grid as a graph where each cell is a node and edges exist between adjacent cells (up, down, left, right).
• The problem becomes one of finding the shortest path in an unweighted graph, which is naturally suited for Breadth-First Search (BFS).

3. Implement BFS Effectively:

• Use BFS to explore all possible paths level by level, ensuring you find the minimum number of minutes required to fix all packages.
• Use a queue to manage the BFS traversal, and employ a dummy position to separate iterations.

4. Optimize Your Solution:

• Ensure the solution has a time complexity of O(r × c), where r is the number of rows and c is the number of columns.
• Aim for a space complexity of O(r × c), which accommodates the grid and the BFS queue.

5. Handle Edge Cases:

• Consider scenarios where it is impossible to fix all packages (e.g., isolated damaged packages).
• Make sure your solution handles small grids, large grids, and grids with varying distributions of good and bad packages.

6. Communicate Your Thought Process:

• During the interview, clearly explain why you chose BFS and how you are managing the traversal.
• Discuss any edge cases and how your solution addresses them.

7. Test Thoroughly:

• Validate your solution with multiple test cases, including edge cases, to ensure its correctness.
• Demonstrate the robustness of your solution by explaining the test cases to your interviewer.

By mastering these concepts and practicing the implementation, you'll be well-prepared to tackle Amazon's "Min Number of Minutes to Fix All Packages" interview question with confidence. Good luck, and remember that clear communication and practice are key to success!