Q1 - Netflix Streaming Content Layout Optimization

In the fast-paced world of streaming, Netflix aims to provide a seamless and engaging user interface. As a front-end engineer at Netflix, you're tasked with optimizing the layout of streaming content tiles on various device screens. The goal is to ensure users can navigate through the vast library with ease and that content is organized efficiently on the grid-based UI.

Your challenge is to write a function that determines the minimum tile area (rectangle) required for showcasing Netflix originals in a dedicated section. These tiles, when clicked, expand to show detailed information about the show. To maintain a clean and uncluttered UI, it's essential to minimize the amount of screen space the tiles take when they are not selected, while still adhering to the aesthetics of Netflix's design.

You are provided with an array of points representing the potential vertices where these rectangular content tiles could be placed within the UI grid. Your function must calculate the smallest possible rectangle that can be formed using any four of these points, thereby optimizing the unexpanded tile space. It's important to note that for the purpose of this task, only rectangles with horizontal and vertical sides are relevant, as the content tiles on Netflix's interface align strictly with the grid and do not include any diagonal positioning (e.g., edges should be vertical and horizontal).

Input:
points = [
  [-3, -1],
  [1, 1],
  [1, 5],
  [2, 1],
  [2, 2],
  [2, 5],
  [2, 6],
  [3, 2],
  [3, 3],
  [3, 5],
  [4, 3],
  [5, -1]
]

Output: 3
The rectangle with vertices: [2, 2], [3, 2], [2, 5], [3, 5] has the minimum area of 3.

Solution

The brute-force method for solving this problem involves a comprehensive search through all possible combinations of four points from the given list to identify a rectangle with the minimum area. Conceptually, this approach involves iterating over each point and treating it as a potential vertex of the rectangle. For every such point, we then explore all possibilities for the second vertex. Subsequently, for each pair of points, we look for a third point, and finally, for each trio, we identify a suitable fourth point.

During this exhaustive process, whenever four points are found that form the vertices of a rectangle, we calculate its area. This area is then compared with the minimum area recorded so far to update our record of the smallest possible rectangle. The time complexity of this approach is O(n⁴), where n represents the total number of points. You know that such a solution would not be acceptable to your interviewers. So, how should we tackle the problem?

This is a challenging problem and has recently become a frequent question in Netflix interviews. Ensure you thoroughly understand our solution, as it not only addresses the challenge at hand but also encapsulates essential principles relevant to similar algorithmic problems.

This problem is complex for several reasons:

1. Multidimensional Optimization: It requires the consideration of both the x and y coordinates to find the smallest rectangle.
2. Algorithm Efficiency: With potentially numerous tiles, the solution must efficiently process these points to be practical for real-time UI adjustments.
3. Geometric Precision: Only rectangles aligned with the grid (vertical and horizontal sides) are relevant, excluding any diagonal positioning.

In our solution, we take a distinct approach by focusing on the concept of diagonals in a rectangle. Unlike other potential solutions that build upon vertical edges formed by points with the same x-coordinate, here we identify rectangles by considering pairs of points that form the diagonals. This technique revolves around the idea that if two points form a diagonal, the other two vertices of the rectangle can be inferred. By checking for the existence of these inferred points and calculating the areas of these identified rectangles, the algorithm effectively discovers the rectangle with the minimum area. This approach, utilizing diagonals, offers an intuitive and efficient alternative to the brute-force strategy, still maintaining optimal computational complexity. You can refer to the illustration below to get an idea of our solution that uses diagonals to infer the existence of rectangles. We will now delve into this solution, examining each key step in detail.

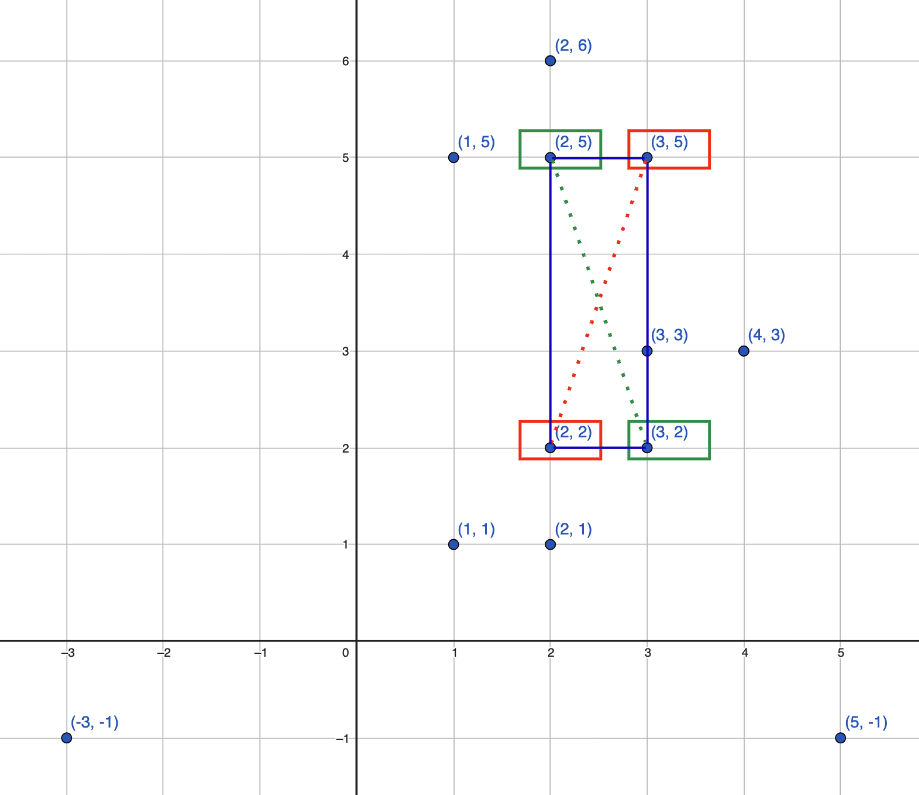
As we will soon discover, the time and space complexity of our solution are O(n²) and O(n), respectively. Additionally, we believe the intuition behind our algorithm is easier to understand compared to other solutions with similar time and space complexities.

1) Constructing Points Set for O(1) look-up time

# Main function.
def min_area_rectangle(points):
    min_area = float('inf')
    # The hash set containing all the points (as strings) for O(1) lookup.
    points_set = construct_points_set(points)
    ...

# Helper method to construct a hash set of all points for O(1) lookup time.
def construct_points_set(points):
    points_set = set()
    for p in points:
        x, y = p
        point_str = str(x) + ":" + str(y) # "x:y"
        points_set.add(point_str)

    return points_set

We call our construct_points_set helper method, which creates a hash set of all points, converting each point into a string format "x:y". This hash set allows for O(1) lookup times when checking if a point exists, optimizing the search process. Each point string (e.g., "x:y") is added to a set. By storing points in this format, the algorithm can quickly check for the existence of specific points, crucial for identifying diagonal counterparts.

2) Iterating Through Points and Checking Diagonals

for i in range(len(points)):
    x1, y1 = points[i]
    for j in range(i + 1, len(points)):
        x2, y2 = points[j]
        # The points need to be diagonal in order for us to find
        # their diagonal counterparts.
        if x1 == x2 or y1 == y2: continue
        # Diagonals exist, calculate the area and compare.
        if diagonals_exist(points_set, x1, y1, x2, y2):
            curr_area = abs(x1 - x2) * abs(y1 - y2)
            min_area = min(min_area, curr_area)

As shown in the code snippet above, we efficiently identify potential rectangles by iterating through each point, pairing it with others to form potential diagonals. For each pair (x1, y1) and (x2, y2), we check if they truly form a diagonal (not aligned horizontally or vertically). For instance, if either x1 == x2 (points are vertically aligned) or y1 == y2 (points are horizontally aligned), then we know that the points are not diagonal.

If the current pair in question - (x1, y1) and (x2, y2) - is indeed diagonal, we use the diagonals_exist function to confirm if the other two vertices, completing the rectangle, exist in our points set. Below is the diagonals_exist function:

# Helper method to determine if the diagonal points for
# (x1, y1) and (x2, y2) exist. The diagonal points would be
# (x1, y2) and (x2, y1) in this case.
def diagonals_exist(points_set, x1, y1, x2, y2):
    # point3 = (x1, y2)
    # point4 = (x2, y1)
    point3_str = str(x1) + ":" + str(y2)
    point4_str = str(x2) + ":" + str(y1)
    return point3_str in points_set and point4_str in points_set

If we have a pair of points (x1, y1) and (x2, y2) forming one diagonal of a rectangle, the other pair that forms the opposite diagonal edge would be (x1, y2) and (x2, y1). These two new points complete the rectangle, with each pair lying on opposite corners. Hence, we verify the existence of the points (x1, y2) and (x2, y1). These points, if present in our points_set, complete the opposite diagonal edge, thus forming a rectangle with the original pair (x1, y1) and (x2, y2). If these complementary diagonal points are found, it confirms we have a valid rectangle. If not, the iteration continues as it indicates that no rectangle can be formed with the current pair of diagonal vertices. Below images show this process using our example:

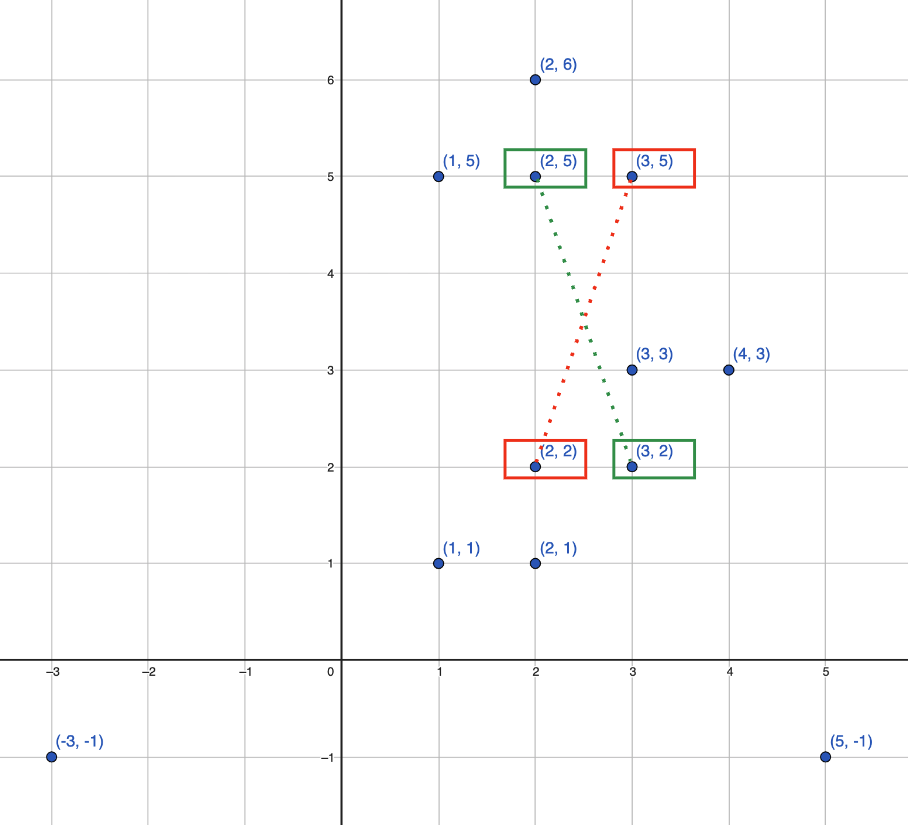
Looking at the image above, suppose (x1, y1) = (2, 2) and (x2, y2) = (3, 5) are highlighted by red boxes. Our diagonals_exist function seeks to find their diagonal counterparts — in this scenario, points highlighted by green boxes. The points in question would be (x1, y2) = (2, 5) and (x2, y1) = (3, 2). We then check if these points are in our points_set. In this case, as the image confirms, they do exist, signifying that we indeed have a valid rectangle formed by these points. The image below illustrates the rectangle formed by our selected points. It visually demonstrates how the identified diagonal pairs and their counterparts come together to create a valid rectangle.

3) Calculating the Area of the Rectangle

# Diagonals exist, calculate the area and compare.
if diagonals_exist(points_set, x1, y1, x2, y2):
    curr_area = abs(x1 - x2) * abs(y1 - y2)
    min_area = min(min_area, curr_area)

When a valid rectangle is found, its area is calculated by multiplying the absolute differences in x and y coordinates of the diagonal points, updating min_area if this area is smaller than the current minimum. This process, pairing each point with others and verifying rectangles, ensures all possibilities are explored. The use of a set for quick point lookups optimizes the algorithm, maintaining its time efficiency.

Complexity Analysis

• Time Complexity: O(n²), where N represents the number of points in our input list.

  Explanation:

  1. Iterating Through Points

     • The solution involves two nested loops iterating over the set of points. The outer loop runs through each point, and for each of these, the inner loop pairs it with every other point. Since the pairing of points is done once for each combination, the total number of operations is proportional to the square of the number of points, leading to O(n²) time complexity.

  2. Checking Diagonals

     • Within these nested loops, the algorithm checks for the existence of diagonal counterparts using the diagonals_exist function. This function has a constant time complexity O(1) because it involves set lookups, which are typically O(1).

• Space Complexity: O(n): The space complexity is largely determined by the points_set, which stores every point as a string. This set's size grows linearly with the number of points. Hence, the space complexity is O(n), where n is the total number of points.

Below is the coding solution for the algorithm we've just explored. We believe this is an easier solution to implement and explain in an interview:

# O(n^2) time | O(n) space
def min_area_rectangle(points):
    min_area = float('inf')
    # The hash set containing all the points (as strings) for O(1) lookup.
    points_set = construct_points_set(points)

    for i in range(len(points)):
        x1, y1 = points[i]
        for j in range(i + 1, len(points)):
            x2, y2 = points[j]
            # The points need to be diagonal in order for us to find
            # their diagonal counterparts.
            if x1 == x2 or y1 == y2: continue
            # Diagonals exist, calculate the area and compare.
            if diagonals_exist(points_set, x1, y1, x2, y2):
                curr_area = abs(x1 - x2) * abs(y1 - y2)
                min_area = min(min_area, curr_area)
                
    return min_area if min_area != float('inf') else 0

# Helper method to construct a hash set of all points for O(1) lookup time.
def construct_points_set(points):
    points_set = set()
    for p in points:
        x, y = p
        point_str = str(x) + ":" + str(y) # "x:y"
        points_set.add(point_str)

    return points_set

# Helper method to determine if the diagonal points for
# (x1, y1) and (x2, y2) exist. The diagonal points would be
# (x1, y2) and (x2, y1) in this case.
def diagonals_exist(points_set, x1, y1, x2, y2):
    # point3 = (x1, y2)
    # point4 = (x2, y1)
    point3_str = str(x1) + ":" + str(y2)
    point4_str = str(x2) + ":" + str(y1)
    return point3_str in points_set and point4_str in points_set

Final Notes

The Minimum Area Rectangle problem, especially in the context of a streaming service's user interface like Netflix, encapsulates several valuable lessons and strategies:

1. Efficient Data Structuring: The challenge underlines the importance of structuring data efficiently. For Netflix, an interface that can swiftly navigate through and display content is vital for user satisfaction.

2. Algorithmic Efficiency and Complexity: The solution emphasizes the importance of developing algorithms that are not only effective in solving the problem but also efficient in terms of computational resources. This reflects real-world constraints where performance and speed are crucial.

3. Spatial Reasoning in UI Design: The problem requires strong spatial reasoning skills to understand and manipulate geometric shapes within a given space, mirroring the skills needed to design user-friendly interfaces.

4. Balancing Complexity and Intuition: Our solution leverages diagonal points, showcasing a balance between algorithmic complexity and intuitive design. This is a key consideration in many software engineering problems.

5. Adaptability and Creativity in Problem-Solving: This solution demonstrates how a problem can be approached from different angles. This adaptability and creativity are valuable in a fast-paced, solution-oriented environment like Netflix.

6. Clear Communication of Complex Ideas: As in this article, clearly articulating the solution to a complex problem is critical, particularly in collaborative team environments prevalent in tech companies.

7. Application to Real-World Scenarios: This problem, while theoretical, has direct applications in real-world scenarios such as optimizing the layout of streaming content in a user interface. It shows the practical relevance of algorithmic problem-solving in enhancing user experience.

Good luck with your interview preparation! This is indeed a challenging question, but armed with the knowledge and understanding of the solution we've discussed, you're well-prepared to tackle it in your interview with Netflix! Also remember that being able to effectively communicate a simpler, yet efficient solution can often be more impressive than struggling with a more complex approach. We hope this solution equips you with the confidence and clarity to handle any follow-up questions from Netflix interviewers.